(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)
An Evidence-Based Proof of Lucas’ Gödelian Thesis and a Definitive Turing Test
Abstract: In this note I detail an evidence-based proof of Lucas’ Gödelian Thesis, and define a definitive Turing Test that differentiates between a human intelligence and a mechanical intelligence.
Introduction
In a paper: `The truth assignments that differentiate human reasoning from mechanistic reasoning: The evidence-based argument for Lucas’ Gödelian thesis’, which appeared in the December 2016 issue of Cognitive Systems Research [An16][1], I briefly addressed the philosophical challenge that arises when an intelligence—whether human or mechanistic—accepts arithmetical propositions as true under an interpretation—either axiomatically or on the basis of subjective self-evidence—without any specified methodology for objectively evidencing such acceptance in the sense of Chetan Murthy and Martin Löb:
“It is by now folklore … that one can view the values of a simple functional language as specifying evidence for propositions in a constructive logic …” … [Mu91][2], Section 1, Introduction.
“Intuitively we require that for each event-describing sentence,  say (i.e. the concrete object denoted by
say (i.e. the concrete object denoted by  exhibits the property expressed by
exhibits the property expressed by  ), there shall be an algorithm (depending on I, i.e.
), there shall be an algorithm (depending on I, i.e. 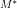 ) to decide the truth or falsity of that sentence.” … [Lob59][3], p.165.
) to decide the truth or falsity of that sentence.” … [Lob59][3], p.165.
Evidence-based reasoning in Arithmetic: Evidence-based reasoning accepts arithmetical propositions as true under an interpretation if, and only if, there is some specified methodology for objectively evidencing such acceptance.
The philosophical ramifications of formally validating John Lucas’ original Gödelian argument in [Lu61][4]—against a reductionist account of the mind—now raise issues (as in [An15b][5]) that lie, and deserve consideration, beyond the formal argumentation of [An16][1].
For instance, the roots of this note lie in the Mechanist’s counter-argument against Lucas’ Gödelian Thesis, as articulated in [An07a][6] (see also [An07b][7] and [An07c][8]; as also this post and this post), which can now be viewed, and refuted, from a broader perspective that admits an evidence-based, Wittgensteinian, distinction between:
(1) mathematically proven, i.e., algorithmically computable (see Appendix B, Definition 2, here), `truth’; and
(2) meta-mathematically proven, i.e., algorithmically verifiable (see Appendix B, Definition 1, here), `truth’;
to which Theorem 1 (below) appeals.
The distinction formalises the reported (see [Lam17][9]) intent underlying Wittgenstein’s objection—in his `notorious’ paragraph in [Wi78][10]—towards conflating mathematical and meta-mathematical entailments, by showing that:
(a) whereas the Mechanist correctly argues (in [An07a][6]) that, for any given numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , a Universal Turing machine can always mathematically prove that Gödel’s arithmetic formula
, a Universal Turing machine can always mathematically prove that Gödel’s arithmetic formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) (as defined in Theorem 1 below) is a theorem in PA;
(as defined in Theorem 1 below) is a theorem in PA;
(b) no Turing machine can mathematically prove that the formula ![[(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) with Gödel number
with Gödel number 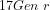 is a theorem in PA; and, ipso facto, meta-mathematically conclude—as a human can—that it could, for any given numeral
is a theorem in PA; and, ipso facto, meta-mathematically conclude—as a human can—that it could, for any given numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , prove that Gödel’s arithmetic formula
, prove that Gödel’s arithmetic formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is a theorem in PA.
is a theorem in PA.
Accordingly, I restrict myself here to merely drawing attention to Lucas’ concluding remarks in an informal defence of his Gödelian Thesis:
“Thus, though the Gödelian formula is not a very interesting formula to enunciate, the Gödelian argument argues strongly for creativity, first in ruling out any reductionist account of the mind that would show us to be, au fond, necessarily unoriginal automata, and secondly by proving that the conceptual space exists in which it (is) intelligible to speak of someone’s being creative, without having to hold that he must be either acting at random or else in accordance with an antecedently specifiable rule”. [Luxx][11].
and to briefly detailing only the import of the evidence-based reasoning introduced in [An12][12] for:
(i) Formally validating Lucas’ Gödelian Thesis as articulated in [An16][1]; and
(ii) Answering affirmatively Alan Turing’s earlier, but related, query in [Tu50][13] as to whether it is possible to definitively differentiate between a human intelligence and a mechanical intelligence.
Validating Lucas’ Gödelian Argument
We begin by noting that the introduction of evidence-based reasoning into the, conflicting, classical (Hilbert’s) and intuitionistic (Brouwer’s) interpretations of quantification (see [An15a][14], Sections 1.1 and 2.1) yields two—hitherto unsuspected and essentially different—well-defined interpretations of the first-order Peano Arithmetic PA (see Appendix A here), over the structure 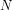 of the natural numbers, which are complementary, and not contradictory (see [An16][1]).
of the natural numbers, which are complementary, and not contradictory (see [An16][1]).
The former yields the classical, weak, standard interpretation 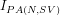 of PA over
of PA over 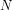 (see Appendix B here), which is non-finitarily well-defined relative to the assignment of weak algorithmically verifiable Tarskian truth values (see Appendix C here) to the compound formulas of PA under
(see Appendix B here), which is non-finitarily well-defined relative to the assignment of weak algorithmically verifiable Tarskian truth values (see Appendix C here) to the compound formulas of PA under 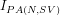 (see [An16][1], Theorem 5.6). The well-definedness follows from the non-finitary proof of consistency for PA detailed in [An16][1], Theorem 5.7.
(see [An16][1], Theorem 5.6). The well-definedness follows from the non-finitary proof of consistency for PA detailed in [An16][1], Theorem 5.7.
The latter yields an unsuspected, strong, finitary interpretation 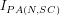 of PA over
of PA over 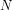 , which is finitarily well-defined relative to the assignment of strong algorithmically computable Tarskian truth values to the compound formulas of PA under
, which is finitarily well-defined relative to the assignment of strong algorithmically computable Tarskian truth values to the compound formulas of PA under 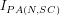 (see [{An16][1], Theorem 6.7). The well-definedness follows from the finitary proof of consistency for PA detailed in [An16][1], Theorem 6.8.
(see [{An16][1], Theorem 6.7). The well-definedness follows from the finitary proof of consistency for PA detailed in [An16][1], Theorem 6.8.
We shall now see that the complementarity can also be viewed as validating Lucas’ Gödelian argument, if we treat it as the claim that (see [An16][1], Thesis 1):
Theorem 1 There can be no mechanist model of human reasoning if the standard interpretation 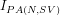 of the first-order Peano Arithmetic PA can be treated as circumscribing the ambit of human reasoning about `true’ arithmetical propositions, and the finitary interpretation
of the first-order Peano Arithmetic PA can be treated as circumscribing the ambit of human reasoning about `true’ arithmetical propositions, and the finitary interpretation 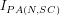 of PA can be treated as circumscribing the ambit of mechanistic reasoning about `true’ arithmetical propositions.
of PA can be treated as circumscribing the ambit of mechanistic reasoning about `true’ arithmetical propositions.
Notation: We use square brackets to differentiate between a symbolic expression—such as ![[(\exists x)P(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cexists+x%29P%28x%29%5D+&bg=ffffff&fg=000000&s=-3&c=20201002) —which denotes a formula of a formal language
—which denotes a formula of a formal language  , and the symbolic expression—such as
, and the symbolic expression—such as 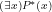 —that denotes its intended meaning under a well-defined interpretation of
—that denotes its intended meaning under a well-defined interpretation of  , where the
, where the  -formula
-formula ![[P(x)]](https://s0.wp.com/latex.php?latex=%5BP%28x%29%5D+&bg=ffffff&fg=000000&s=-3&c=20201002) interprets as the relation
interprets as the relation 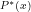 .
.
Proof: We note that Kurt Gödel has shown meta-mathematically how to construct an arithmetical formula with a single variable, say ![[R(x)]](https://s0.wp.com/latex.php?latex=%5BR%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) —Gödel refers to this formula only by its Gödel number
—Gödel refers to this formula only by its Gödel number  in [Go31][15], p.25(12)—such that:
in [Go31][15], p.25(12)—such that:
![\bullet [R(x)]](https://s0.wp.com/latex.php?latex=%5Cbullet+%5BR%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is not PA-provable; but
is not PA-provable; but
![\bullet [R(n)]](https://s0.wp.com/latex.php?latex=%5Cbullet+%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is PA-provable for any PA numeral
is PA-provable for any PA numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) .
.
Hence, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , Gödel’s primitive recursive relation
, Gödel’s primitive recursive relation ![xB \lceil [R(n)] \rceil](https://s0.wp.com/latex.php?latex=xB+%5Clceil+%5BR%28n%29%5D+%5Crceil+&bg=ffffff&fg=000000&s=-2&c=20201002) must hold for some natural number
must hold for some natural number  :
:
 where
where 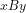 denotes Gödel’s primitive recursive relation (see [Go31][15], p. 22(45)):
denotes Gödel’s primitive recursive relation (see [Go31][15], p. 22(45)):
` is the Gödel-number of a proof sequence in PA whose last term is the PA formula with Gödel-number
is the Gödel-number of a proof sequence in PA whose last term is the PA formula with Gödel-number  ‘;
‘;
 and
and ![\lceil [R(n)] \rceil](https://s0.wp.com/latex.php?latex=%5Clceil+%5BR%28n%29%5D+%5Crceil+&bg=ffffff&fg=000000&s=-2&c=20201002) denotes the Gödel-number of
denotes the Gödel-number of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) ;
;
We also note (see [An16][1], Theorem 2.1), that we cannot conclude finitarily from Tarski’s definitions (see Appendix C, Definitions 3 to 10 here) whether, or not, a quantified PA formula ![[(\forall x)F(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cforall+x%29F%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is algorithmically verifiable as always true, under
is algorithmically verifiable as always true, under 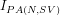 , if
, if ![[F(x)]](https://s0.wp.com/latex.php?latex=%5BF%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is algorithmically verifiable (see Appendix B, Definition 1 here) under
is algorithmically verifiable (see Appendix B, Definition 1 here) under 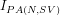 , but not algorithmically computable (see Appendix B, Definition 2 here) under
, but not algorithmically computable (see Appendix B, Definition 2 here) under 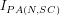 .
.
Now:
(i) Since Gödel has shown meta-mathematically that the PA-formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is PA-provable for any PA-numeral
is PA-provable for any PA-numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , it follows that:
, it follows that:
(a) For any natural number  , there is always a deterministic algorithm which will provide evidence that the interpretation
, there is always a deterministic algorithm which will provide evidence that the interpretation 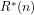 of
of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) under
under 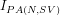 is an algorithmically verifiable true arithmetical proposition.
is an algorithmically verifiable true arithmetical proposition.
Moreover:
(ii) By [An16][1], Corollary 8.2, the formula ![[\neg(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cneg%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is provable in PA. Hence, since PA is finitarily consistent (see [An16], Theorem 6.8), we can mathematically conclude, under
is provable in PA. Hence, since PA is finitarily consistent (see [An16], Theorem 6.8), we can mathematically conclude, under 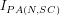 , that:
, that:
(a) There is no deterministic algorithm which, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , will provide evidence that the interpretation
, will provide evidence that the interpretation 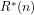 of
of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) under
under 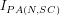 is an algorithmically computable true arithmetical proposition.
is an algorithmically computable true arithmetical proposition.
However:
(iii) Since PA is also non-finitarily consistent (see [An16][1], Theorem 5.7), we cannot contradict (i)(a) by non-finitarily interpreting quantification under 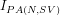 and mathematically concluding from the PA-provability of the formula
and mathematically concluding from the PA-provability of the formula ![[\neg(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cneg%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) either that:
either that:
(a) For some unspecified natural number  , there is a deterministic algorithm which provides evidence that the interpretation
, there is a deterministic algorithm which provides evidence that the interpretation 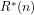 of
of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) under
under 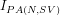 is not an algorithmically verifiable true arithmetical proposition.
is not an algorithmically verifiable true arithmetical proposition.
or that:
(b) For some unspecified natural number  , there is no deterministic algorithm which will provide evidence that the interpretation
, there is no deterministic algorithm which will provide evidence that the interpretation 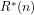 of
of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) under
under 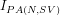 is an algorithmically verifiable true arithmetical proposition.
is an algorithmically verifiable true arithmetical proposition.
Instead:
(iv) By [An16][1], Corollary 8.3, we can only conclude, under 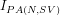 , that the PA-provability of the formula
, that the PA-provability of the formula ![[\neg(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cneg%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) implies that we cannot mathematically conclude from the axioms and rules of inference of PA that:
implies that we cannot mathematically conclude from the axioms and rules of inference of PA that:
(a) For any natural number  , there is always a deterministic algorithm which will provide evidence that the interpretation
, there is always a deterministic algorithm which will provide evidence that the interpretation 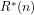 of
of ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) under
under 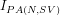 is an algorithmically verifiable true arithmetical proposition.
is an algorithmically verifiable true arithmetical proposition.
If we now assume that the finitary interpretation 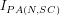 of PA can be treated as circumscribing the ambit of mechanistic reasoning about `true’ arithmetical propositions, whence any mechanical witness can only reason mathematically—i.e., finitarily from the PA axioms and rules of inference, as in (iv) (see [An16][1], Theorem 7.1)—then although, for any numeral
of PA can be treated as circumscribing the ambit of mechanistic reasoning about `true’ arithmetical propositions, whence any mechanical witness can only reason mathematically—i.e., finitarily from the PA axioms and rules of inference, as in (iv) (see [An16][1], Theorem 7.1)—then although, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , a mechanical witness can give evidence under the finitary interpretation
, a mechanical witness can give evidence under the finitary interpretation 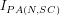 that the PA formula
that the PA formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) holds in
holds in 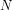 , no mechanical witness can conclude finitarily under the finitary interpretation
, no mechanical witness can conclude finitarily under the finitary interpretation 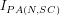 of PA that, for any numeral
of PA that, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , the PA formula
, the PA formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) holds in
holds in 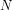 (since, by Corollary 8.2 in [An16][1], the formula
(since, by Corollary 8.2 in [An16][1], the formula ![[\neg (\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cneg+%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is provable in PA).
is provable in PA).
Whereas, if we assume that the standard interpretation 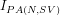 of PA can be treated as circumscribing the ambit of human reasoning about `true’ arithmetical propositions—whence a human witness can also reason meta-mathematically, i.e., non-finitarily, from the PA axioms and rules of inference, as in (i)—then a human witness can conclude under the non-finitary standard interpretation
of PA can be treated as circumscribing the ambit of human reasoning about `true’ arithmetical propositions—whence a human witness can also reason meta-mathematically, i.e., non-finitarily, from the PA axioms and rules of inference, as in (i)—then a human witness can conclude under the non-finitary standard interpretation 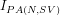 of PA that, for any numeral
of PA that, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , the PA formula
, the PA formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) holds in
holds in 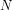 . The theorem follows. …
. The theorem follows. … 
Significance of differentiating between strong algorithmically computable truth, and weak algorithmically verifiable truth
We note that the importance of differentiating between:
(i) the strong, algorithmically computable, `truth’—of the provable formulas of a formal mathematical language 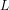 —which follows by finitary mathematical reasoning from the axioms and rules of inference of
—which follows by finitary mathematical reasoning from the axioms and rules of inference of 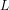 under a well-defined interpretation; and
under a well-defined interpretation; and
(ii) the weak, algorithmically verifiable, `truth’—of the provable formulas of 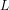 —which follows by non-finitary meta-mathematical reasoning from the axioms and rules of inference of
—which follows by non-finitary meta-mathematical reasoning from the axioms and rules of inference of 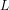 under a well-defined interpretation;
under a well-defined interpretation;
is:
(a) reflected in Thoralf Skolem’s ([Sk22][16], p.295) cautionary remarks against inviting paradox by conflating entailments of different formal systems over different domains;
(b) implicit in, and an essential component of, Lampert’s interpretation of Ludwig Wittgenstein’s objection—in the latter’s `notorious’ paragraph in [Wi78][10]—to the conclusions that Gödel drew from his undifferentiated mathematical/meta-mathematical reasoning in [Go31][15]:
“The most crucial aspect of any comparison of two different types of unprovability proofs is the question of what serves as the “criterion of unprovability” (I, Section 15). According to Wittgenstein, such a criterion should be a purely syntactic criteria independent of any meta-mathematical interpretation of formulas. It is algorithmic proofs relying on nothing but syntactic criteria that serve as a measure for assessing meta-mathematical interpretations, not vice-versa.” … [Lam17][9]
A definitive Turing Test
“Let us fix our attention on one particular digital computer C. Is it true that by modifying this computer to have an adequate storage, suitably increasing its speed of action, and providing it with an appropriate programme, C can be made to play satisfactorily the part of A in the imitation game, the part of B being taken by a man? \ldots In short, then, there might be men cleverer than any given machine, but then again there might be other machines cleverer again, and so on.” … [Tu50][13], Section 5 and Objection (3).
Theorem 1 can also be viewed as a definitive Turing Test between a logician and any Turing machine TM.
In other words, we can demonstrate that the algorithmically computable architecture of any conceivable Turing machine (digital computer) has inherent limitations which constrain it from answering the following Query in the affirmative; whereas the human brain is not constrained similarly.
Query 1: Can you prove that, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , Gödel’s arithmetic formula
, Gödel’s arithmetic formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is a theorem in the first-order Peano Arithmetic PA, where
is a theorem in the first-order Peano Arithmetic PA, where ![[R(x)]](https://s0.wp.com/latex.php?latex=%5BR%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is defined by its Gödel number
is defined by its Gödel number  in eqn.12, and
in eqn.12, and ![[(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is defined by its Gödel number
is defined by its Gödel number 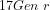 in eqn.13, on p.25 of [Go31][15]? Answer only either `Yes’ or `No’.
in eqn.13, on p.25 of [Go31][15]? Answer only either `Yes’ or `No’.
Logician: Yes.
By Gödel’s meta-mathematical reasoning on p.26(2) of [Go31][15], a logician can conclude, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , that the formula
, that the formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is a theorem in PA; even though the formula
is a theorem in PA; even though the formula ![[(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is not a theorem in PA.
is not a theorem in PA.
TM: No.
By Corollary 8.2 in [An16][1], the formula ![[\neg (\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%5Cneg+%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is provable in PA and so, by Theorem 7.1 in [An16], no Turing machine can prove that the formula
is provable in PA and so, by Theorem 7.1 in [An16], no Turing machine can prove that the formula ![[(\forall x)R(x)]](https://s0.wp.com/latex.php?latex=%5B%28%5Cforall+x%29R%28x%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) with Gödel number
with Gödel number 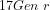 is a theorem in PA and, ipso facto, conclude that, for any numeral
is a theorem in PA and, ipso facto, conclude that, for any numeral ![[n]](https://s0.wp.com/latex.php?latex=%5Bn%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) , Gödel’s arithmetic formula
, Gödel’s arithmetic formula ![[R(n)]](https://s0.wp.com/latex.php?latex=%5BR%28n%29%5D+&bg=ffffff&fg=000000&s=-2&c=20201002) is a theorem in PA.
is a theorem in PA.
Appendix A: The Peano Arithmetic PA
Appendix B: The Two Interpretations of PA
Appendix C: Tarski’s Inductive Definitions
References
Return to 1 [An16] Anand, B. S. 2016. The truth assignments that differentiate human reasoning from mechanistic reasoning: The evidence-based argument for Lucas’ Gödelian thesis. In Cognitive Systems Research, 40. Elsevier.
Return to 2 [Mu91] Murthy, C. R. 1991. An evaluation semantics for classical proofs. In Proceedings of Sixth IEEE Symposium on Logic in Computer Science, 96–109. Also Cornell TR 91-1213, 1991.
Return to 3 [Lob59] Löb, M. H. 1959. Constructive Truth. In Proceedings of the Colloquium Held at Amsterdam, 1957, Studies in Logic and the Foundations of Mathematics, Eds. L. E. J. Brouwer, E.W. Beth, A. Heyting, Constructivity in Mathematics, A. Heyting (ed.), pp.159-168, North-Holland Publishing Company, Amsterdam.
Return to 4 [Lu61] Lucas, J. R. 1961. Minds, Machines and Gödel. Philosophy XXXVI:112–127. Reprinted in The Modeling of Mind. Kenneth M.Sayre and Frederick J.Crosson, eds., Notre Dame Press, 1963, pp.269-270; and Minds and Machines, ed. Alan Ross Anderson, Prentice-Hall, 1964, pp.43-59.
Return to 5 [An15b] Anand, B. S. 2015. Algorithmically Verifiable Logic vis à vis Algorithmically Computable Logic: Could resolving EPR need two complementary Logics? Paper presented on 26’th June at the Workshop on Emergent Computational Logics at UNILOG’2015, 5th World Congress and School on Universal Logic, 20th June 2015 – 30th June 2015, University of Istanbul, Istanbul, Turkey.
Return to 6 [An07a] Anand, B. S. 2007. The Mechanist’s Challege. The Reasoner, Vol(1)5 p5-6.
Return to 7 [An07b] Anand, B. S. 2007. Why we shouldn’t fault Lucas and Penrose for continuing to believe in the Gödelian argument against computationalism – I. The Reasoner, Vol(1)6 p3-4.
Return to 8 [An07c] Anand, B. S. 2007. Why we shouldn’t fault Lucas and Penrose for continuing to believe in the Gödelian argument against computationalism – II. The Reasoner, Vol(1)7 p2-3.
Return to 9 [Lam17] Lampert, T. 2017. Wittgenstein and Gödel: An Attempt to Make “Wittgenstein’s Objection” Reasonable. In Philosophia Mathematica. nkx017.
Return to 10 [Wi78] Wittgenstein, L. 1937. Remarks on the Foundations of Mathematics. Cambridge: MIT Press, 1978 edition.
Return to 11 [Luxx] Lucas, J. R. 19xx. The Gödelian Argument: Turn Over the Page. Web essay.
Return to 12 [An12] Anand, B. S. 2012. Evidence-based Interpretations of PA. In Proceedings of the Symposium on Computational Philosophy at the AISB/IACAP World Congress 2012-Alan Turing 2012, 2-6 July 2012. University of Birmingham, Birmingham, UK.
Return to 13 [Tu50] Turing, A. M. 1950. Computing Machinery and Intelligence. In Mind, Volume LIX, Issue 236, 1 October 1950:433–460.
Return to 14 [An15a] Anand, B. S. 2015. Why Hilbert’s and Brouwer’s interpretations of quantification are complementary and not contradictory. In Epsilon 2015 Workshop on Hilbert’s Epsilon and Tau in Logic, Informatics and Linguistics, 10th June 2015 – 12th June 2015. Paper presented on 10th June at the University of Montpellier, Montpellier, France.
Return to 15 [Go31] Gödel, K. 1931. On formally undecidable propositions of Principia Mathematica and related systems I. Translated from the German original by Elliott Mendelson. In Martin Davis (ed.), The Undecidable, 1965. Dover edition 2004, pp.5-38, Dover Publications Inc., Mineola, NY 1150.
Return to 16 [Sk22] Skolem, T. 1922. Some remarks on axiomatized set theory. Text of an address delivered in Helsinki before the Fifth Congress of Scandinavian Mathematicians, 4-7 August 1922. In Jean van Heijenoort (ed.) From Frege to Gödel: A source book in Mathematical Logic, 1878 – 1931, 1967 edition, pp.464-479, Harvard University Press, Cambridge, Massachusetts.
References in Appendices
[Ba16] Bauer, A. 2016. Five Stages of Accepting Constructive Mathematics. In Bull. Math. Soc. (N. S.). Electronically published on October 3, 2016.
[Ct75] Chaitin, G. J. 1975. A Theory of Program Size Formally Identical to Information Theory. In Journal of the ACM (JACM), volume 22, Issue 3, July 1975, pp.329-340. Association for Computing Machinery, New York.
[Ct82] Chaitin, G. J. 1982. Gödel’s Theorem and Information. In International Journal of Theoretical Physics, volume 21, pp.941-954. Kluwer Academic Publishers-Plenum Publishers.
[Hi27] Hilbert, D. 1927. The Foundations of Mathematics. Text of an address delivered in July 1927 at the Hamburg Mathematical Seminar. In Jean van Heijenoort (ed.) From Frege to Gödel: A source book in Mathematical Logic, 1878 – 1931, 1967 edition, pp.464-479, Harvard University Press, Cambridge, Massachusetts.
[Me64] Mendelson, E. 1964. Introduction to Mathematical Logic. Princeton: Van Norstrand, 1964 edition.



Recent comments