Category Archive

You are currently browsing the category archive for the ‘Theory of Numbers’ category.

The significance of evidence-based reasoning for Computational Complexity

December 20, 2018 in computational complexity, Foundations of mathematics, Foundations of mathematics, logic and computation, logic and computation, Philosophy, Theory of Numbers | Tags: algorithmically computable, algorithmically verifiable, Aristotle's particularisation, arithmetic, Church Turing Thesis, completed infinity, computationalism, consistency, constructive, determinism, EPR paradox, extra-terrestrial, finitary, first order, FOL, formal, formal language, foundations, Gödel, Gödelian argument, Goodstein, Hilbert, human, human intelligence, logic, Lucas, mathematical truth, mathematics, mechanical intelligence, mechanist, natural numbers, omega-consistency, para-consistency, Peano Arithmetic PA, philosophy, reasoning, Rosser, Rule C, science, semantic, SETI, simple functional language, standard interpretation, syntactic, Tarski, Turing, undecidable, unpredictability | Leave a comment

Why primality is polynomial time, but factorisation is not

Differentiating between the signature of a number and its value

A brief review: The significance of evidence-based reasoning

In a paper: `The truth assignments that differentiate human reasoning from mechanistic reasoning: The evidence-based argument for Lucas’ Gödelian thesis’, which appeared in the December 2016 issue of Cognitive Systems Research [An16], I briefly addressed the philosophical challenge that arises when an intelligence—whether human or mechanistic—accepts arithmetical propositions as true under an interpretation—either axiomatically or on the basis of subjective self-evidence—without any specified methodology for objectively evidencing such acceptance in the sense of Chetan Murthy and Martin Löb:

“It is by now folklore … that one can view the values of a simple functional language as specifying evidence for propositions in a constructive logic …” … Chetan. R. Murthy: [Mu91], \S 1 Introduction.

“Intuitively we require that for each event-describing sentence, $\phi_{o^{\iota}}n_{\iota}$ say (i.e. the concrete object denoted by $n_{\iota}$ exhibits the property expressed by $\phi_{o^{\iota}}$ ), there shall be an algorithm (depending on I, i.e. $M^{*}$ ) to decide the truth or falsity of that sentence.” … Martin H Löb: [Lob59], p.165.

Definition 1 (Evidence-based reasoning in Arithmetic): Evidence-based reasoning accepts arithmetical propositions as true under an interpretation if, and only if, there is some specified methodology for objectively evidencing such acceptance.

The significance of introducing evidence-based reasoning for assigning truth values to the formulas of a first-order Peano Arithmetic, such as PA, under a well-defined interpretation (see Section 3 in [An16]), is that it admits the distinction:

(1) algorithmically verifiable `truth’ (Definition 2}); and

(2) algorithmically computable `truth’ (Definition 3).

Definition 2 (Deterministic algorithm): A deterministic algorithm computes a mathematical function which has a unique value for any input in its domain, and the algorithm is a process that produces this particular value as output.

Note that a deterministic algorithm can be suitably defined as a `realizer‘ in the sense of the Brouwer-Heyting-Kolmogorov rules (see [Ba16], p.5).

For instance, under evidence-based reasoning the formula $[(\forall x)F(x)]$ of the first-order Peano Arithmetic PA must always be interpreted weakly under the classical, standard, interpretation of PA (see [An16], Theorem 5.6) in terms of algorithmic verifiability (see [An16], Definition 1); where, if the PA-formula $[F(x)]$ interprets as an arithmetical relation $F^{*}(x)$ over $N$ :

Definition 2 (Algorithmic verifiability): The number-theoretical relation $F^{*}(x)$ is algorithmically verifiable if, and only if, for any natural number $n$ , there is a deterministic algorithm $AL_{(F,\ n)}$ which can provide evidence for deciding the truth/falsity of each proposition in the finite sequence $\{F^{*}(1), F^{*}(2), \ldots, F^{*}(n)\}$ .

Whereas $[(\forall x)F(x)]$ must always be interpreted strongly under the finitary interpretation of PA (see [An16], Theorem 6.7) in terms of algorithmic computability ([An16], Definition 2), where:

Definition 3 (Algorithmic computability): The number theoretical relation $F^{*}(x)$ is algorithmically computable if, and only if, there is a deterministic algorithm $AL_{F}$ that can provide evidence for deciding the truth/falsity of each proposition in the denumerable sequence $\{F^{*}(1), F^{*}(2), \ldots\}$ .

The significance of the distinction between algorithmically computable reasoning based on algorithmically computable truth, and algorithmically verifiable reasoning based on algorithmically verifiable truth, is that it admits the following, hitherto unsuspected, consequences:

(i) PA has two well-defined interpretations over the domain $N$ of the natural numbers (including $0$ ):

(a) the weak non-finitary standard interpretation $I_{PA(N, SV)}$ ([An16], Theorem 5.6),

and

(b) a strong finitary interpretation $I_{PA(N, SC)}$ ([An16], Theorem 6.7);

(ii) PA is non-finitarily consistent under $I_{PA(N, SV)}$ ([An16], Theorem 5.7);

(iii) PA is finitarily consistent under $I_{PA(N, SC)}$ ([An16], Theorem 6.8).

The significance of evidence-based reasoning for Computational Complexity

In this investigation I now show the relevance of evidence-based reasoning, and of distinguishing between algorithmically verifiable and algorithmically computable number-theoretic functions (as defined above), for Computational Complexity is that it assures us a formal foundation for placing in perspective, and complementing, an uncomfortably counter-intuitive entailment in number theory—Theorem 2 below—which has been treated by conventional wisdom as sufficient for concluding that the prime divisors of an integer cannot be proven to be mutually independent.

However, I show there that such informally perceived barriers are, in this instance, illusory; and that admitting the above distinction illustrates:

(a) Why the prime divisors of an integer are mutually independent Theorem 2;

(b) Why determining whether the signature (Definition 3 below) of a given integer $n$ —coded as the key in a modified Bazeries-cylinder (see Definition 7 of this paper) based combination lock—is that of a prime, or not, can be done in polynomial time $O(log_{_{e}}n)$ (Corollary 4 of this paper); as compared to the time $\ddot{O}(log_{_{e}}^{15/2}n)$ given by Agrawal et al in [AKS04], and improved to $\ddot{O}(log_{_{e}}^{6}n)$ by Lenstra and Pomerance in [LP11], for determining whether the value of a given integer $n$ is that of a prime or not.

Definition 4 (Signature of a number): The signature of a given integer $n$ is the sequence $a_{_{n,i}}$ where $n + a_{_{n,i}} \equiv 0\ mod\ (p_{_{i}})$ for all primes $p_{_{i}}\ such\ that\ 1\leq i \leq \pi(\sqrt{n})$ .

Unique since, if $p_{_{\pi(\sqrt{m})+1}}^{2} > m \geq p_{_{\pi(\sqrt{m})}}^{2}$ and $p_{_{\pi(\sqrt{n})+1}}^{2} > n \geq p_{_{\pi(\sqrt{n})}}^{2}$ have the same signature, then $|m - n| = c_{_{1}}.\prod_{i=1}^{\pi(\sqrt{m})}p_{_{i}} = c_{_{2}}.\prod_{i=1}^{\pi(\sqrt{n})}p_{_{i}}$ ; whence $c_{_{1}} = c_{_{2}} = 0$ since $\prod_{i=1}^{k}p_{_{i}} > (\prod_{i=2}^{k-2}p_{_{i}}).p_{_{k}}^{^{2}} > p_{_{k+1}}^{2}$ for $k > 4$ by appeal to Bertrand’s Postulate $2.p_{_{k}} > p_{_{k+1}}$ ; and the uniqueness is easily verified for $k \leq 4$ .

Definition 5 (Value of a number): The value of a given integer $n$ is any well-defined interpretation—over the domain of the natural numbers—of the (unique) numeral $[n]$ that represents $n$ in the first-order Peano Arithmetic PA.

We note that Theorem 2 establishes a lower limit for [AKS04] and [LP11], because determining the signature of a given integer $n$ does not require knowledge of the value of the integer as defined by the Fundamental Theorem of Arithmetic.

Theorem 1: (Fundamental Theorem of Arithmetic): Every positive integer $n > 1$ can be represented in exactly one way as a product of prime powers:

$n=p_{1}^{n_{1}}p_{2}^{n_{2}}\cdots p_{k}^{n_{k}}=\prod _{i=1}^{k}p_{i}^{n_{i}}$

where $p_{1} < p_{2} < \ldots < p_{k}$ are primes and the $n_{i}$ are positive integers (including $0$ ).

Are the prime divisors of an integer mutually independent?

In this paper I address the query:

Query 1: Are the prime divisors of an integer $n$ mutually independent?

Definition 6 (Independent events): Two events are independent if the occurrence of one event does not influence (and is not influenced by) the occurrence of the other.

Intuitively, the prime divisors of an integer seem to be mutually independent by virtue of the Fundamental Theorem of Arithmetic

Moreover, the prime divisors of $n$ can also be seen to be mutually independent in the usual, linearly displayed, Sieve of Eratosthenes, where whether an integer $n$ is crossed out as a multiple of a prime $p$ is obviously independent of whether it is also crossed out as a multiple of a prime $q \neq p$ :

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19 …

Despite such compelling evidence, conventional wisdom appears to accept as definitive the counter-intuitive conclusion that although we can see it as true, we cannot mathematically prove the following proposition as true:

Proposition 1: Whether or not a prime $p$ divides an integer $n$ is independent of whether or not a prime $q \neq p$ divides the integer $n$ .

We note that such an unprovable-but-intuitively-true conclusion makes a stronger assumption than that in Gödel’s similar claim for his arithmetical formula $[(\forall x)R(x)]$ —whose Gödel-number is $17Gen\ r$ —in [Go31], p.26(2). Stronger, since Gödel does not assume his proposition to be intuitively true, but shows that though the arithmetical formula with Gödel-number $17Gen\ r$ is not provable in his Peano Arithmetic $P$ yet, for any $P$ -numeral $[n]$ , the formula $[R(n)]$ whose Gödel-number is $Sb \left(r \begin{array}{c}17 \\ Z(n)\end{array}\right)$ is $P$ -provable, and therefore meta-mathematically true under any well-defined Tarskian interpretation of $P$ (cf., [An16], Section 3.).

Expressed in computational terms (see [An16], Corollary 8.3), under any well-defined interpretation of $P$ , Gödel’s formula $[R(x)]$ translates as an arithmetical relation, say $R'(x)$ , such that $R'(n)$ is algorithmically verifiable, but not algorithmically computable, as always true over $N$ , since $[\neg (\forall x)R(x)]$ is $P$ -provable ([An16], Corollary 8.2).

We thus argue that a perspective which denies Proposition 1 is based on perceived barriers that reflect, and are peculiar to, only the argument that:

Theorem 2: There is no deterministic algorithm that, for any given $n$ , and any given prime $p \geq 2$ , will evidence that the probability $\mathbb{P}(p\ |\ n)$ that $p$ divides $n$ is $\frac{1}{p}$ , and the probability $\mathbb{P}(p\not|\ n)$ that $p$ does not divide $n$ is $1 - \frac{1}{p}$ .

Proof By a standard result in the Theory of Numbers ([Ste02], Chapter 2, p.9, Theorem 2.1, we cannot define a probability function for the probability that a random $n$ is prime over the probability space $(1, 2, 3, \ldots, )$ .

(Compare with the informal argument in [HL23], pp.36-37.)

In other words, treating Theorem 2 as an absolute barrier does not admit the possibility—which has consequences for the resolution of outstanding problems in both the theory of numbers and computational complexity—that Proposition 1 is algorithmically verifiable, but not algorithmically computable, as true, since:

Theorem 3: For any given $n$ , there is a deterministic algorithm that, given any prime $p \geq 2$ , will evidence that the probability $\mathbb{P}(p\ |\ n)$ that $p$ divides $n$ is $\frac{1}{p}$ , and the probability $\mathbb{P}(p\not|\ n)$ that $p$ does not divide $n$ is $1 - \frac{1}{p}$ .

Author’s working archives & abstracts of investigations

Why the prime divisors of an integer are mutually independent

July 20, 2016 in Foundations of mathematics, logic and computation, Theory of Numbers | Tags: arithmetic, logic, mathematics, natural numbers | Leave a comment

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

A: A conventional perspective on why the prime divisors of an integer are not mutually independent

In a post Getting to the Roots of Factoring on the blog Gödel’s Lost Letter and P = NP (hosted jointly by him and Professor of Computer Science at Georgia Tech College of Computing, Richard Lipton) Professor of Computer Science and Engineering at the University of Buffalo, Kenneth W. Regan `revisits’ a 1994 paper on factoring by his co-host.

What I find intriguing in the above post is that the following extract subsumes, almost incidentally, a possibly implicit belief which may be inhibiting not only a resolution of the computational complexity of Integer Factoring (see this investigation) by conventional methods but, for similar reasons, also resolution of a large class of apparently unrelated problems (see, for instance, this investigation and this previous post):

“Here is the code of the algorithm. … the input $x$ is a product of two prime numbers, $\phi$ is a polynomial in just one variable, and $\gcd$ refers to the greatest-common-divisor algorithm expounded by Euclid around 300 B.C. …

$\star$ Repeat until exit:

$\star\ a :=$ a random number in $1,\dots, x-1$ ;

$\star\ b := \phi(a)\ mod(x)$ ;

$\star$ if $(\gcd(b,x) > 1)$ then exit.

Exiting enables carrying out the two prime factors of $x$ …

How many iterations must one expect to make through this maze before exit? How and when can the choice of the polynomial $\phi$ speed up the exploration? …

Note that we cannot consider the events $b \equiv 0\ mod(p)$ and $b \equiv 0\ mod(q)$ to be independent, even though $p$ and $q$ are prime, because $b = \phi(a)$ and $\phi$ may introduce bias.”

The following reasoning shows why it is not obvious whether the assertion that:

“… we cannot consider the events $b \equiv 0\ mod(p)$ and $b \equiv 0\ mod(q)$ to be independent”

is intended to narrowly reflect a putative proof in the particular context of the assertion, or to echo a more general belief.

B: Defining the probability that a given integer is divisible by a given smaller integer

(1) We consider the questions:

(a) What is the probability for any given $n>i>1$ and $i \geq 0$ , where $i>u \geq 0$ , that:

$n+u \equiv\ 0\ (mod\ i)$ ?

(b) What is the compound probability for any given $n>i,\ j>1$ , where $i \neq j$ , $i>u \geq 0$ , and $j>v \geq 0$ , that:

$n+u \equiv\ 0\ (mod\ i)$ , and $n+v \equiv\ 0\ (mod\ j)$ ?

(c) What is the compound probability for any given $n>i,\ j>1$ , where $i \neq j$ , $i>u \geq 0$ , and $j>v \geq 0$ , that:

$i$ divides $n+u$ , and $j$ divides $n+v$ ?

C: Why the prime divisors of an integer are mutually independent

(2) We note that:

(a) The answer to query (1a) above is that the probability the roll of an $i$ -sided cylindrical die will yield the value $u$ is $\frac{1}{i}$ by the probability model for such an event as definable over the probability space $(0, 1, 2, \ldots, i-1)$ ;

(b) The answer to query (1b) above is that the probability the simultaneous roll of one $i$ -sided cylindrical die and one $j$ -sided cylindrical die will yield the values $u$ and $v$ , respectively, is $\frac{1}{i.j}$ by the probability model for such a simultaneous event as defined over the probability space $\{(u, v): i > u \geq 0, j > v \geq 0\}$ .

(3) We trivially conclude that:

The compound probability of determining $u$ and $v$ correctly from the simultaneous roll of one $i$ -sided cylindrical die and one $j$ -sided cylindrical die, is the product of the probability of determining $u$ correctly from the roll of an $i$ -sided cylindrical die, and the probability of determining $v$ correctly from the roll of a $j$ -sided cylindrical die.

(4) We further conclude non-trivially that the answer to query (1c) above is given by:

(a) If $i$ and $j$ are co-prime, the compound probability of correctly determining that $i$ divides $n$ and $j$ divides $n$ from the simultaneous roll of one $i$ -sided cylindrical die and one $j$ -sided cylindrical die, is the product of the probability of correctly determining that $i$ divides $n$ from the roll of an $i$ -sided cylindrical die, and the probability of correctly determining that $j$ divides $n$ from the roll of a $j$ -sided cylindrical die.

(b) The assumption that $i$ and $j$ be co-prime is also necessary, since 4(a) would not always be the case if $i$ and $j$ were not co-prime.

For instance, let $j=2i$ . The probability that an $i$ -sided cylindrical die will then yield $0$ —and allow us to conclude that $i$ divides $n$ —is $\frac{1}{i}$ , and the probability that a $j$ -sided cylindrical die will then yield $0$ —and allow us to conclude that $j$ divides $n$ —is $\frac{1}{j}$ ; but the probability of determining both that $i$ divides $n$ , and that $j$ divides $n$ , from a simultaneous roll of the two cylindrical dice is $\frac{1}{j}$ , and not $\frac{1}{i.j}$ .

(5) We thus conclude non-trivially that, if $p$ and $q$ are two unequal primes, the probability of determining whether $p$ divides $n$ is independent of the probability of determining whether $q$ divides $n$ .

Author’s working archives & abstracts of investigations

42_Resolving_EPR_UNILOG_2013_Extended_Abstract

Why there are infinitely many twin primes

July 19, 2016 in Foundations of mathematics, logic and computation, Theory of Numbers | Tags: arithmetic, mathematics | Leave a comment

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

A: The twin prime conjecture

In the post Notes on the Bombieri asymptotic sieve on his blog What’s new, 2006 Fields Medal awardee and Professor of Mathematics at UCLA, Terence Tao, writes and comments that:

“The twin prime conjecture, still unsolved, asserts that there are infinitely many primes $p$ such that $p+2$ is also prime. A more precise form of this conjecture is (a special case) of the Hardy-Littlewood prime tuples conjecture, which asserts that:

$\sum_{n \leq x} \Lambda(n) \Lambda(n+2) = (2\Pi_2+o(1)) x$ … (1)

as $x \rightarrow \infty$ , where $\Lambda$ is the von Mangoldt function and $\Pi_2 = 0.6606\dots$ is the twin prime constant:

$\prod_{p>2} (1 - \frac{1}{(p-1)^2})$ .

Because $\Lambda$ is almost entirely supported on the primes, it is not difficult to see that (1) implies the twin prime conjecture.

One can give a heuristic justification of the asymptotic (1) (and hence the twin prime conjecture) via sieve theoretic methods. …

It may also be possible that the twin prime conjecture could be proven by non-analytic means, in a way that does not lead to significantly new estimates on the sum $\sum_{n \leq x} \Lambda(n) \Lambda(n+2)$ (though this sum will of course have to go to infinity as $x \to \infty$ if the twin prime conjecture holds).”

B: Why heuristic approaches to the twin prime conjecture may not suffice

1. What seems to prevent a non-heuristic determination of the limiting behaviour of prime counting functions is that the usual approximations of $\pi(n)$ for finite values of $n$ are apparently derived from real-valued functions which are asymptotic to $\pi(x)$ , such as $\frac{x}{log_{e}x}$ , $Li(x)$ and Riemann’s function $R(x) = \sum_{n=1}^{\infty}\frac{\mu(n)}{(n)}li(x^{1/n})$ .

2. The degree of approximation for finite values of $n$ is thus determined only heuristically, by conjecturing upon an error term in the asymptotic relation that can be seen to yield a closer approximation than others to the actual values of $\pi(n)$ .

3. Moreover, currently, conventional approaches to evaluating prime counting functions for finite $n$ may also subscribe to the belief:

(i) either—explicitly (see here)—that whether or not a prime $p$ divides an integer $n$ is not independent of whether or not a prime $q \neq p$ divides the integer $n$ ;

(ii) or—implicitly (since the twin-prime problem is yet open)—that a proof to the contrary must imply that if $P(n\ is\ a\ prime)$ is the probability that $n$ is a prime, then $\sum_{_{i = 1}}^{^{\infty}} P(i\ is\ a\ prime) = 1$ .

4. If so, then conventional approaches seem to conflate the two probabilities:

(i) The probability $P(a)$ of selecting a number that has the property of being prime from a given set $S$ of numbers;

Example 1: I have a bag containing $100$ numbers in which there are twice as many composites as primes. What is the probability that the first number you blindly pick from it is a prime. This is the basis for setting odds in games such as roulette.

(ii) The probability $P(b)$ of determining that a given integer $n$ is prime.

Example 2: I give you a $5$ -digit combination lock along with a $10$ -digit number $n$ . The lock only opens if you set the combination to a proper factor of $n$ which is greater than $1$ . What is the probability that the first combination you try will open the lock. This is the basis for RSA encryption, which provides the cryptosystem used by many banks for securing their communications.

5. In case 4(i), if the precise proportion of primes to non-primes in $S$ is definable, then clearly $P(a)$ too is definable.

However if $S$ is the set $N$ of all integers, and we cannot define a precise ratio of primes to composites in $N$ , but only an order of magnitude such as $O(\frac{1}{log_{_{e}}n})$ , then equally obviously $P(a)$ cannot be defined in $N$ (see Chapter 2, p.9, Theorem 2.1, here).

6. In case 4(ii) it follows that $P(b) = \frac{1}{\pi(\sqrt{n})}$ , since we can show (see Corollary 2.9 on p.14 of this investigation) that whether or not a prime $p$ divides a given integer $n$ is independent of whether or not a prime $q \neq p$ divides $n$ .

7. We thus have that $\pi(n) \approx n.\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ . Hence, even though we cannot define the probability $P(n\ is\ a\ prime)$ of selecting a number from the set $N$ of all natural numbers that has the property of being prime, $\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ can be treated as the de facto probability that a given $n$ is prime.

8. Moreover, by considering the asymptotic density of the set of all integers that are not divisible by the first $\pi(\sqrt {n})$ primes $p_{_{1}}, p_{_{2}}, \ldots, p_{_{\pi(\sqrt {n})}}$ we can show that, for any $n$ , the expected number of such integers in any interval of length $(p_{_{\pi(\sqrt{ n})+1}}^{2} - p_{_{\pi(\sqrt n)}}^{2})$ is:

$(p_{_{\pi(\sqrt{ n})+1}}^{2} - p_{_{\pi(\sqrt n)}}^{2})\prod_{i = 1}^{\pi(\sqrt{n})}(1 - \frac{1}{p_{_{i}}})$ .

9. We can then show that a non-heuristic approximation for the number of primes less than or equal to $n$ is given for all $n$ by:

$\pi(n) \approx \sum_{j = 1}^{n}\prod_{i = 1}^{\pi(\sqrt{j})}(1 - \frac{1}{p_{_{i}}}) \sim a.\frac{n}{log_{e}n} \rightarrow \infty$

for some constant $a > 2.e^{-\gamma} \approx 1.12292 \ldots$ .

10. We can show, similarly, that the expected number of Dirichlet and twin primes in the interval ( $p_{_{\pi(\sqrt {n})}}^{2},\ p_{_{\pi(\sqrt{ n})+1}}^{2}$ ) can be estimated similarly; and conclude that the number of such primes $\leq n$ is, in each case, cumulatively approximated non-heuristically by a function that $\rightarrow \infty$ .

11. The method can, moreover, be generalised to apply to a large class of prime counting functions (see Section 5.A on p.22 of this investigation).

C: A non-heuristic proof that there are infinitely many twin primes

1. In particular, instead of estimating:

$\sum_{_{n \leq x}}\Lambda(n)\Lambda(n+2)$

heuristically by analytic considerations, one could also estimate the number $\pi_{_{2}}(x)$ of twin primes $\leq x$ non-heuristically as:

$\sum_{_{n \leq x}}P(n).P(n+2)$

where $P(n)$ is the de facto probability that a given $n$ is prime; and where we need to allow for the possibility that the two probabilities may not be independent.

2. One way of approaching this would be to define an integer $n$ as a $\mathbb{TW}(k)$ integer if, and only if, $r_{p_{_{i}}}(n) \neq 0$ and $r_{p_{_{i}}}(n) \neq 2$ for all $1 \leq i \leq k$ , where $0 \leq r_{_{i}}(n) \leq i-1$ is defined for all $i \geq 0$ by:

$n + r_{_{i}}(n) \equiv 0\ (mod\ i)$

3. Note that if $n$ is a $\mathbb{TW}(k)$ integer, then both $n$ and $n+2$ are not divisible by any of the first $k$ primes $\{p_{_{1}}, p_{_{2}}, \ldots, p_{_{k}}\}$ .

4. The asymptotic density of $\mathbb{TW}(k)$ integers over the set of natural numbers is then:

$\mathbb{D}(\mathbb{TW}(k)) = \prod_{i=2}^{k}(1 - \frac{2}{p_{_{i}}})$ .

5. Further, if $p_{_{k}}^{2} \leq n \leq p_{_{k+1}}^{2}$ is a $\mathbb{TW}(k)$ integer, then $n$ is a prime and either $n+2$ is also a prime, or $n+2 = p_{_{k +1}}^{2}$ .

6. If we define $\pi_{_{\mathbb{TW}(k)}}(n)$ as the number of $\mathbb{TW}(k)$ integers $\leq n$ , the expected number of $\mathbb{TW}(k)$ integers in any interval $(a, b)$ is given by:

$\pi_{_{\mathbb{TW}(k)}}(b) - \pi_{_{\mathbb{TW}(k)}}(a) \approx (b-a)\prod_{i=2}^{k}(1 - \frac{2}{p_{_{i}}})$

7. Since $\pi_{_{\mathbb{TW}(k)}}(p_{_{k+1}}^{2}) - \pi_{_{\mathbb{TW}(k)}}(p_{_{k}}^{2})$ is at most one less than the number of twin-primes in the interval $(p_{_{k+1}}^{2} - p_{_{k}}^{2})$ , it follows that:

$\pi_{_{\mathbb{TW}(k)}}(p_{_{k+1}}^{2}) - \pi_{_{\mathbb{TW}(k)}}(p_{_{k}}^{2}) + 1 \geq \pi_{_{2}}(p_{_{k+1}}^{2}) - \pi_{_{2}}(p_{_{k)}}^{2}) \geq \pi_{_{\mathbb{TW}(k)}}(p_{_{k+1}}^{2}) - \pi_{_{\mathbb{TW}(k)}}(p_{_{k}}^{2})$

8. Now, the expected number of $\mathbb{TW}(k)$ integers in the interval $(p_{_{k+1}}^{2} - p_{_{k}}^{2})$ is given by:

$\pi_{_{\mathbb{TW}(k)}}(p_{_{k+1}}^{2}) - \pi_{_{\mathbb{TW}(k)}}(p_{_{k}}^{2}) \approx (p_{_{k+1}}^{2} - p_{_{k}}^{2})\prod_{i=2}^{k}(1 - \frac{2}{p_{_{i}}})$ .

9. We conclude that the number $\pi_{_{2}}(p_{_{k+1}}^{2})$ of twin primes $\leq p_{_{k+1}}^{2}$ is given by the cumulative non-heuristic approximation:

$\sum_{j=1}^{k} (\pi_{_{2}}(p_{_{j+1}}^{2}) - \pi_{_{2}}(p_{_{j}}^{2})) = \pi_{_{2}}(p_{_{k+1}}^{2}) \approx \sum_{j=1}^{k} (p_{_{j+1}}^{2} - p_{_{j}}^{2})\prod_{i=2}^{j}(1 - \frac{2}{p_{_{i}}}) \rightarrow \infty$ .

Author’s working archives & abstracts of investigations

Can Primes yield a heuristic model of quantum behaviour?

July 7, 2016 in Education, Foundations of mathematics, logic and computation, logic and computation, Philosophy, Quantum Physics, Theory of Numbers | Tags: algorithmically computable, algorithmically verifiable, ambiguity, arithmetic, computation, computationalism, consistency, constructive, determinism, EPR paradox, finitary, first order, formal, formal language, foundations, Gödel, Hilbert, human, human intelligence, languages of adequate expression, languages of effective communication, logic, logical paradoxes, mathematical objects, mathematical truth, mathematics, mechanical intelligence, mechanist, natural numbers, Peano Arithmetic PA, peano axioms, philosophy, reasoning, science, standard interpretation, Tarski, truth, Turing | Leave a comment

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

We investigate whether the probabilistic distribution of prime numbers can be treated as a heuristic model of quantum behaviour, since it too can be treated as a quantum phenomena, with a well-defined binomial probability function that is algorithmically computable, where the conjectured values of $\pi(n)$ differ from actual values with a binomial standard deviation, and where we define a phenomena as a quantum phenomena if, and only if, it obeys laws that can only be represented mathematically by functions that are algorithmically verifiable, but not algorithmically computable.

1. Thesis: The concept of ‘mathematical truth’ must be accountable

The thesis of this investigation is that a major philosophical challenge—which has so far inhibited a deeper understanding of the quantum behaviour reflected in the mathematical representation of some laws of nature (see, for instance, this paper by Eamonn Healey)—lies in holding to account the uncritical acceptance of propositions of a mathematical language as true under an interpretation—either axiomatically or on the basis of subjective self-evidence—without any specified methodology of accountability for objectively evidencing such acceptance.

2. The concept of ‘set-theoretical truth’ is not accountable

Since current folk lore is that all scientific truths can be expressed adequately, and communicated unambiguously, in the first order Set Theory ZF, and since the Axiom of Infinity of ZF cannot—even in principle—be objectively evidenced as true under any putative interpretation of ZF (as we argue in this post), an undesirable consequence of such an uncritical acceptance is that the distinction between the truths of mathematical propositions under interpretation which can be objectively evidenced, and those which cannot, is not evident.

3. The significance of such accountability for mathematics

The significance of such a distinction for mathematics is highlighted in this paper due to appear in the December 2016 issue of Cognitive Systems Research, where we address this challenge by considering the two finitarily accountable concepts of algorithmic verifiability and algorithmic computability (first introduced in this paper at the Symposium on Computational Philosophy at the AISB/IACAP World Congress 2012-Alan Turing 2012, Birmingham, UK).

(i) Algorithmic verifiability

A number-theoretical relation $F(x)$ is algorithmically verifiable if, and only if, for any given natural number $n$ , there is an algorithm $AL_{(F,\ n)}$ which can provide objective evidence for deciding the truth/falsity of each proposition in the finite sequence $\{F(1), F(2), \ldots, F(n)\}$ .

(ii) Algorithmic computability

A number theoretical relation $F(x)$ is algorithmically computable if, and only if, there is an algorithm $AL_{F}$ that can provide objective evidence for deciding the truth/falsity of each proposition in the denumerable sequence $\{F(1), F(2), \ldots\}$ .

(iii) Algorithmic verifiability vis à vis algorithmic computability

We note that algorithmic computability implies the existence of an algorithm that can decide the truth/falsity of each proposition in a well-defined denumerable sequence of propositions, whereas algorithmic verifiability does not imply the existence of an algorithm that can decide the truth/falsity of each proposition in a well-defined denumerable sequence of propositions.

From the point of view of a finitary mathematical philosophy—which is the constraint within which an applied science ought to ideally operate—the significant difference between the two concepts could be expressed by saying that we may treat the decimal representation of a real number as corresponding to a physically measurable limit—and not only to a mathematically definable limit—if and only if such representation is definable by an algorithmically computable function (Thesis 1 on p.9 of this paper that was presented on 26th June at the workshop on Emergent Computational Logics at UNILOG’2015, 5th World Congress and School on Universal Logic, Istanbul, Turkey).

We note that although every algorithmically computable relation is algorithmically verifiable, the converse is not true.

We show in the CSR paper how such accountability helps define finitary truth assignments that differentiate human reasoning from mechanistic reasoning in arithmetic by identifying two, hitherto unsuspected, Tarskian interpretations of the first order Peano Arithmetic PA, under both of which the PA axioms interpret as finitarily true over the domain $N$ of the natural numbers, and the PA rules of inference preserve such truth finitarily over $N$ .

4. The ambit of human reasoning vis à vis the ambit of mechanistic reasoning

One corresponds to the classical, non-finitary, putative standard interpretation of PA over $N$ , and can be treated as circumscribing the ambit of human reasoning about ‘true’ arithmetical propositions.

The other corresponds to a finitary interpretation of PA over $N$ that circumscibes the ambit of mechanistic reasoning about ‘true’ arithmetical propositions, and establishes the long-sought for consistency of PA (see this post); which establishes PA as a mathematical language of unambiguous communication for the mathematical representation of physical phenomena.

5. The significance of such accountability for the mathematical representation of physical phenomena

The significance of such a distinction for the mathematical representation of physical phenomena is highlighted in this paper that was presented on 26th June at the workshop on Emergent Computational Logics at UNILOG’2015, 5th World Congress and School on Universal Logic, Istanbul, Turkey, where we showed how some of the seemingly paradoxical elements of quantum mechanics may resolve if we define:

Quantum phenomena: A phenomena is a quantum phenomena if, and only if, it obeys laws that can only be represented mathematically by functions that are algorithmically verifiable but not algorithmically computable.

6. The mathematical representation of quantum phenomena that is determinate but not predictable

By considering the properties of Gödel’s $\beta$ function (see $\S$ 4.1 on p.8 of this preprint)—which allows us to strongly represent any non-terminating sequence of natural numbers by an arithmetical function—it would follow that, since any projection of the future values of a quantum-phenomena-associated, algorithmically verifiable, function is consistent with an infinity of algorithmically computable functions, all of whose past values are identical to the algorithmically verifiable past values of the function, the phenomena itself would be essentially unpredicatable if it cannot be represented by an algorithmically computable function.

However, since the algorithmic verifiability of any quantum phenomena shows that it is mathematically determinate, it follows that the physical phenomena itself must observe determinate laws.

7. Such representation does not need to admit multiverses

Hence (contrary to any interpretation that admits unverifiable multiverses) only one algorithmically computable extension of the function is consistent with the law determining the behaviour of the phenomena, and each possible extension must therefore be associated with a probability that the next observation of the phenomena is described by that particular extension.

8. Is the probability of the future behaviour of quantum phenomena definable by an algorithmically computable function?

The question arises: Although we cannot represent quantum phenomena explicitly by an algorithmically computable function, does the phenomena lend itself to an algorithmically computable probability of its future behaviour in the above sense?

9. Can primes yield a heuristic model of quantum behaviour?

We now show that the distribution of prime numbers denoted by the arithmetical prime counting function $\pi(n)$ is a quantum phenomena in the above sense, with a well-defined probability function that is algorithmically computable.

10. Two prime probabilities

We consider the two probabilities:

(i) The probability $P(a)$ of selecting a number that has the property of being prime from a given set $S$ of numbers;

(ii) The probability $P(b)$ of determining a proper factor of a given number $n$ .

11. The probability of a randomly chosen number from the set of natural numbers is not definable

Clearly the probability $P(a)$ of selecting a number that has the property of being prime from a given set $S$ of numbers is definable if the precise proportion of primes to non-primes in $S$ is definable.

However if $S$ is the set $N$ of all integers, and we cannot define a precise ratio of primes to composites in $N$ , but only an order of magnitude such as $O(\frac{1}{log_{_{e}}n})$ , then equally obviously $P(a) = P(n\ is\ a\ prime)$ cannot be defined in $N$ (see Chapter 2, p.9, Theorem 2.1, here).

12. The prime divisors of a natural number are independent

Now, the following paper proves $P(b) = \frac{1}{\pi(\sqrt{n})}$ , since it shows that whether or not a prime $p$ divides a given integer $n$ is independent of whether or not a prime $q \neq p$ divides $n$ :

Why Integer Factorising cannot be polynomial time

We thus have that $\pi(n) \approx n.\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ , with a binomial standard deviation.

Hence, even though we cannot define the probability $P(n\ is\ a\ prime)$ of selecting a number from the set $N$ of all natural numbers that has the property of being prime, $\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ can be treated as the putative non-heuristic probability that a given $n$ is a prime.

13. The distribution of primes is a quantum phenomena

The distribution of primes is thus determinate but unpredictable, since it is representable by the algorithmically verifiable but not algorithmically computable arithmetical number-theoretic function $Pr(n) = p_{_{n}}$ , where $p_{_{n}}$ is the $n$ ‘th prime.

The Prime Number Generating Theorem and the Trim and Compact algorithms detailed in this 1964 investigation illustrate why the arithmetical number-theoretic function $Pr(n)$ is algorithmically verifiable but not algorithmically computable (see also this Wikipedia proof that no non-constant polynomial function $Pr(n)$ with integer coefficients exists that evaluates to a prime number for all integers $n$ .).

Moreover, although the distribution of primes is a quantum phenomena with probabilty $\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ , it is easily seen (see Figs. 7-11 on pp.23-26 of this preprint) that the generation of the primes is algorithmically computable.

14. Why the universe may be algorithmically computable

By analogy, this suggests that although the measurable values of some individual properties of particles in the universe over time may represent a quantum phenomena, the universe itself may be algorithmically computable if the laws governing the generation of all the particles in the universe over time are algorithmically computable.

Author’s working archives & abstracts of investigations

The PvNP problem: Why we need to review current approaches towards determining the computational complexity of Integer Factorising

July 2, 2016 in Foundations of mathematics, logic and computation, logic and computation, Theory of Numbers | Tags: algorithm, arithmetic, complete system of residues, computation, computational complexity, incongruent residues, independent events, integer factorising, logic, mathematics, modular arithmetic, mutually independent divisors, natural numbers, polynomial-time, probability of being a prime, PvNP | Leave a comment

Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

1. Since, by the Prime Number Theorem, the number of primes $\leq \sqrt n$ is $O(\frac{\sqrt n}{log_{_{e}}\sqrt n})$ , it would follow that determining a factor of $n$ requires at least one logical operation for each prime $\leq \sqrt n$ , and therefore cannot be done in polynomial time—whence $P \neq NP$ —IF whether or not a prime $p$ divides an integer $n$ were independent of whether or not a prime $q \neq p$ divides the integer $n$ .

2. Currently, conventional approaches to determining the computational complexity of Integer Factorising apparently appeal critically to the belief that:

(i) either—explicitly (see here)—that whether or not a prime $p$ divides an integer $n$ is not independent of whether or not a prime $q \neq p$ divides the integer $n$ ;

(ii) or—implicitly (since the problem is yet open)—that a proof to the contrary must imply that if $P(n\ is\ a\ prime)$ is the probability that $n$ is a prime, then $\sum_{_{i = 1}}^{^{\infty}} P(i\ is\ a\ prime) = 1$ .

3. If so, then conventional approaches seem to conflate the two probabilities:

(i) The probability $P(a)$ of selecting a number that has the property of being prime from a given set $S$ of numbers;

(ii) The probability $P(b)$ of determining that a given integer $n$ is prime.

4. In case 3(i), if the precise proportion of primes to non-primes in $S$ is definable, then clearly $P(a)$ too is definable.

5. In case 3(ii) the following paper proves $P(b) = \frac{1}{\pi(\sqrt{n})}$ , since it shows that whether or not a prime $p$ divides a given integer $n$ is independent of whether or not a prime $q \neq p$ divides $n$ :

Why Integer Factorising cannot be polynomial time

Not only does it immediately follow that $P \neq NP$ (see here), but we further have that $\pi(n) \approx n.\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ , with a binomial standard deviation. Hence, even though we cannot define the probability $P(n\ is\ a\ prime)$ of selecting a number from the set $N$ of all natural numbers that has the property of being prime, $\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ can be treated as the de facto probability that a given $n$ is prime, with all its attended consequences for various prime-counting functions and the Riemann Zeta function (see here).

Author’s working archives & abstracts of investigations

Three intriguing non-heuristic prime counting function queries

May 26, 2016 in Theory of Numbers | Tags: algorithm, complete system of residues, computing, computational complexity, integer factorising, incongruent residues, mutually independent divisors, logic, modular arithmetic, natural number, number | Leave a comment

$Updated: 05/11/2018$

1 The Riemann Hypothesis (see also this paper) reflects the fact that all currently known approximations of the number $\pi(n)$ of primes $\leq n$ are heuristic

All known approximations of the number $\pi(n)$ of primes $\leq n$ are currently derived from real-valued functions that are asymptotic to $\pi(x)$ , such as $\frac{x}{log_{e}x}$ , $Li(x)$ and Riemann’s function $R(x) = \sum_{n=1}^{\infty}\frac{\mu(n)}{(n)}li(x^{1/n})$ , where the degree of approximation for finite values of $n$ is determined only heuristically by conjecturing upon an error term in the asymptotic relation that can be `seen’, but not yet proven, to yield `good’ approximations of $\pi(n)$ (as described, for instance, by Barry Mazur and William Stein on p.36 of their absorbingly written, but without sacrificing rigour, entry-level book Prime Numbers and the Riemann Hypothesis).

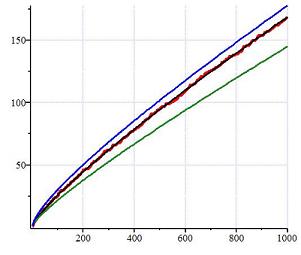
PiAndOthers

The above graph compares the actual number $\pi(x)$ (red) of primes $\leq x$ with the distribution of primes as estimated variously by the functions $Li(x)$ (blue), $R(x)$ (black), and $\frac{x}{log_{e}x}$ (green), where $R(x)$ is Riemann’s function $\sum_{n=1}^{\infty}\frac{\mu(n)}{(n)}li(x^{1/n})$ .

1A Two non-heuristic approximations of the number $\pi(n)$ of primes $\leq n$

The following introduces, and compares, two non-heuristic prime counting functions (investigated more fully here) that, prima facie, yield non-heuristic approximations of $\pi(n)$ :

(i) $\pi_{_{H}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}}) = n.\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}})$ (green); and

(ii) $\pi_{_{L}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{j}}(1-\frac{1}{p_{_{i}}})$ (red);

Based on manual and spreadsheet calculations, Figs.1 and 2 compare the values of the two non-heuristically estimated prime counting functions with the actual values of $\pi(n)$ (blue) for $4 \leq n \leq 1500$ and $4 \leq n \leq 3000$ .

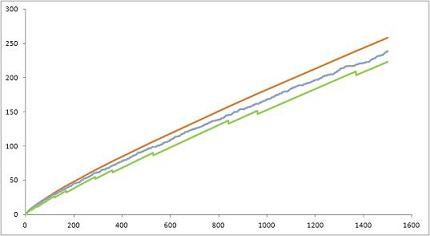
Primes_less_than_n_1500_A

Fig.1: The above graph compares the non-heuristically estimated values of $\pi_{_{H}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}}) = n.\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}})$ (green) and $\pi_{_{L}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{j}}(1-\frac{1}{p_{_{i}}})$ (red) vs the actual values of $\pi(n)$ (blue) for $4 \leq n \leq 1500$ .

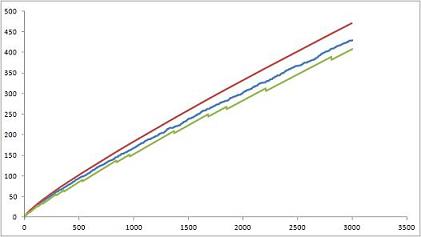
Primes_less_than_n_3000

Fig.2: The above graph compares the non-heuristically estimated values of $\pi_{_{H}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}}) = n.\prod_{i=1}^{\sqrt{n}}(1-\frac{1}{p_{_{i}}})$ (green) and $\pi_{_{L}}(n) = \sum_{j=1}^{n}\prod_{i=1}^{\sqrt{j}}(1-\frac{1}{p_{_{i}}})$ (red) vs the actual values of $\pi(n)$ (blue) for $4 \leq n \leq 3000$ . Note that the gradient of both $y = \pi_{_{H}}(x)$ and of $y = \pi_{_{L}}(x)$ in the interval $(p_{_{n}}^{2},\ p_{_{n+1}}^{2})$ is $\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}}) \rightarrow 0$ .

1B Three intriguing queries

Since $\pi(n) \sim \frac{n}{log_{e}(n)}$ (by the Prime Number Theorem), whilst $\pi_{_{H}}(n) \sim 2e^{-\gamma}\frac{n}{log_{_{e}}n}$ (by Mertens’ Theorem, where $\gamma$ is the Euler-Mascheroni constant and $2.e^{-\gamma} \approx 1.12292 \ldots$ ), and it can be shown (see Corollary 3.2 here) that $\pi_{_{L}}(n) \sim ae^{-\lambda}\frac{n}{log_{_{e}}n}$ for some $a \geq 2$ , this raises the interesting queries (see also $\S$ 2 of this initial investigation):

Fig_3

Fig.3. The overlapping rectangles $A, B, C, D, \ldots$ represent $\pi_{_{H}}(p_{_{j+1}}^{2}) = p_{_{j+1}}^{2}.\prod_{i = 1}^{j}(1 - \frac{1}{p_{_{i}}})$ for $j \geq 1$ . Figures within each rectangle are the primes and estimated primes corresponding to the functions $\pi(n)$ and $\pi_{_{H}}(n)$ , respectively, within the interval $(1,\ p_{_{j+1}}^{2})$ for $j \geq 2$ .

Fig_4

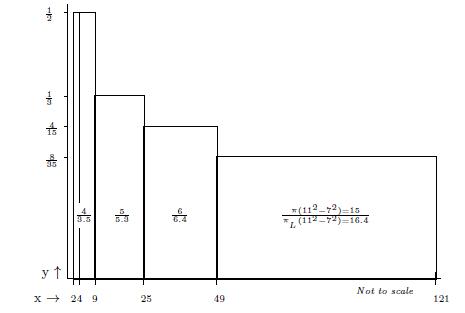
Fig.4: Graph of $y = \prod_{i = 1}^{\pi(\sqrt{x})}(1 - \frac{1}{p_{_{i}}})$ . The rectangles represent $(p_{_{j+1}}^{2} - p_{_{j}}^{2})\prod_{i = 1}^{j}(1 - \frac{1}{p_{_{i}}})$ for $j \geq 1$ . Figures within each rectangle are the primes corresponding to the functions $\pi(n)$ and $\pi_{_{L}}(n)$ within the interval $(p_{_{j}}^{2},\ p_{_{j+1}}^{2})$ for $j \geq 2$ . The area under the curve is $\pi_{_{L}}(x) = (x - p_{_{n}}^{2})\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}}) + \sum_{j = 1}^{n-1}(p_{_{j+1}}^{2} - p_{_{j}}^{2})\prod_{i = 1}^{j}(1 - \frac{1}{p_{_{i}}}) + 2$ .

(a) Which is the least $n$ , if any, such that $\pi_{_{H}}(n) > \pi(n)$ ?

(b) Which is the largest $n$ , if any, such that $\pi(n) > \pi_{_{H}}(n)$ ?

(c) Is $\pi(n) / \frac{n}{log_{_{e}}n}$ an algorithmically verifiable, but not algorithmically computable (see Definitions 1 and 2 here), function which is discontinuous in the limit $n \rightarrow \infty$ (in the sense of Zeno’s paradox in 2-dimensions considered in Case 4 here)?

1C Three intriguing observations

Eulp_nlogn_M003_00

Fig.5: The above graph compares the actual values of $\pi(n)$ in the range $4 \leq n \leq 100$ , with $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ in the range $4 \leq n \leq 110$ , and $\frac{n}{log_{_{e}}\ n}$ in the range $4 \leq n \leq 120$ .

Eulp_nlogn_M003_01

Fig.6: The above graph compares the actual values of $\pi(n)$ in the range $4 \leq n \leq 1000$ , with $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ in the range $4 \leq n \leq 1100$ , and $\frac{n}{log_{_{e}}\ n}$ in the range $4 \leq n \leq 1200$ .

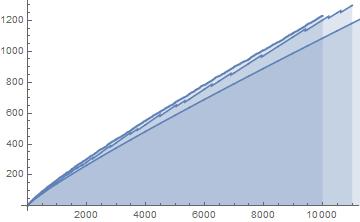
Eulp_nlogn_M003_02

Fig.7: The above graph compares the actual values of $\pi(n)$ in the range $4 \leq n \leq 10000$ , with $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ in the range $4 \leq n \leq 11000$ , and $\frac{n}{log_{_{e}}\ n}$ in the range $4 \leq n \leq 12000$ .

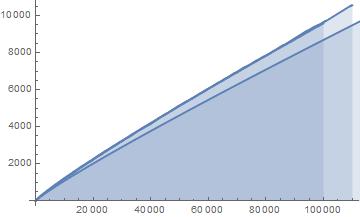
Eulp_nlogn_M003_03

Fig.8: The above graph compares the actual values of $\pi(n)$ in the range $4 \leq n \leq 100000$ , with $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ in the range $4 \leq n \leq 110000$ , and $\frac{n}{log_{_{e}}\ n}$ in the range $4 \leq n \leq 120000$ .

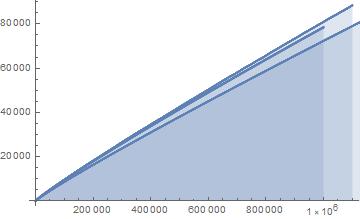
Eulp_nlogn_M003_04

Fig.9: The above graph compares the actual values of $\pi(n)$ in the range $4 \leq n \leq 1000000$ , with $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ in the range $4 \leq n \leq 1100000$ , and $\frac{n}{log_{_{e}}\ n}$ in the range $4 \leq n \leq 1200000$ .

Query (a) is answered by Figs.8-9, which show that the least $n$ such that $\pi_{_{H}}(n) > \pi(n)$ occurs somewhere around $n = 100000$ .

As regards Query (b) however, we conjecture that Fig.9 suggests that there is no larger $n$ such that $\pi(n) > \pi_{_{H}}(n)$ .

Finally, we conjecture that—despite what is suggested by the Prime Number Theorem—Query (c) can be answered affirmatively if the three functions $\pi(n)$ , $n.\prod_{_{j=i}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{j}}})$ , and $\frac{n}{log_{_{e}}\ n}$ are as well-behaved as Fig.9 suggests!

2 Density of integers not divisible by primes $Q = \{q_{_{1}}, q_{_{2}}, \ldots, q_{_{k}}\}$

The above observations reflect the circumstance that (formal proofs for the following are detailed in Chapters 34 and 35 here):

Lemma 2.1: The asymptotic density of the set of all integers that are not divisible by any of a given set of primes $Q = \{q_{_{1}}, q_{_{2}}, \ldots, q_{_{k}}\}$ is:

$\prod_{q \in Q}(1-1/q)$ .

It follows that:

Lemma 2.2: The expected number of integers in any interval $(a,b)$ that are not divisible by any of a given set of primes $Q = \{q_{_{1}}, q_{_{2}}, \ldots, q_{_{k}}\}$ is:

$(b-a)\prod_{q \in Q}(1-1/q)$ .

2A The function $\pi_{_{H}}(n)$

In particular, the expected number $\pi_{_{H}}(n)$ of integers $\leq n$ that are not divisible by any of the first $k$ primes $p_{_{1}}, p_{_{2}}, \ldots, p_{_{k}}$ is:

Corollary 2.3: $\pi_{_{H}}(n) = n.\prod_{i = 1}^{k}(1 - \frac{1}{p_{_{i}}})$

It follows that:

Corollary 2.4: The expected number of primes $\leq p_{_{\pi(\sqrt n)+1}}^{2}$ is:

$\pi_{_{H}}(p_{_{\pi(\sqrt n)+1}}^{2}) = p_{_{\pi(\sqrt n) +1}}^{2}\prod_{i = 1}^{\pi(\sqrt n)}(1 - \frac{1}{p_{_{i}}})$

We conclude that $\pi_{_{H}}(n)$ is a non-heuristic approximation of the number of primes $\leq n$ :

Lemma 2.5: $\pi(n) \approx \pi_{_{H}}(n) = n.\prod_{i = 1}^{\pi(\sqrt{n})}(1 - \frac{1}{p_{_{i}}}) \sim 2e^{-\gamma}\frac{n}{log_{_{e}}n}$ .

2B The function $\pi_{_{L}}(n)$

We note similarly that:

Corollary 2.6: The expected number of primes in the interval ( $p_{_{\pi(\sqrt n)}}^{2},\ p_{_{\pi(\sqrt n)+1}}^{2}$ ) is:

$(p_{_{\pi(\sqrt n)+1}}^{2} - p_{_{\pi(\sqrt n)}}^{2})\prod_{i = 1}^{\pi(\sqrt n)}(1 - \frac{1}{p_{_{i}}})$ .

It further follows from Lemma 2.2 and Corollary 2.6 that:

Corollary 2.7: The number $\pi(p_{_{\pi(\sqrt n)+1}}^{2})$ of primes less than $p_{_{\pi(\sqrt n)+1}}^{2}$ is cumulatively approximated by:

$\pi_{_{L}}(p_{_{\pi(\sqrt n)+1}}^{2}) = \sum_{j=1}^{\pi(\sqrt n)}\{(p_{_{j+1}}^{2} - p_{_{j}}^{2})\prod_{i = 1}^{j}(1 - \frac{1}{p_{_{i}}})\}$ .

We conclude that $\pi_{_{L}}(n)$ is also a cumulative non-heuristic approximation of the number of primes $\leq n$ :

Lemma 2.8: $\pi(n) \approx \pi_{_{L}}(n) = \sum_{j = 1}^{n}\prod_{i = 1}^{\pi(\sqrt{j})}(1 - \frac{1}{p_{_{i}}})$ .

2C An apparent paradox

We note that since the above non-heuristic estimates appeal to an asymptotic density, and the density of primes tends to $0$ as $n \rightarrow \infty$ , Figs.1-9 suggest that:

(i) $\pi_{_{L}}(n)$ overestimates $\pi(n)$ cumulatively over each of the intervals; whilst

(ii) $\pi_{_{H}}(n)$ overestimates $\pi(n)$ over a single cumulative interval.

even though Fig.3 suggests that:

$\bullet$ The number of primes in any interval $(p_{_{j}}^{2},\ p_{_{j+1}}^{2})$ for any given $j < n$ is constant as $n \rightarrow \infty$ ; but

$\bullet$ The contribution of the expected number of primes in the interval $(p_{_{j}}^{2},\ p_{_{j+1}}^{2})$ to the total expected number (see Corollary 2.4), $\pi_{_{H}}(p_{_{n+1}}^{2}) = p_{_{n+1}}^{2}.\prod_{i = 1}^{n+1}(1 - \frac{1}{p_{_{i}}})$ , of primes in the interval $(1,\ p_{_{n+1}}^{2})$ decreases monotonically.

In other words, an apparent paradox surfaces (as suggested by Fig.9) when we express $\pi(n)$ and the function $\pi_{_{H}}(n)$ in terms of the number of primes determined by each function respectively in each interval $(p_{_{n}}^{2},\ p_{_{n+1}}^{2})$ as follows:

$\pi(p_{_{n+1}}^{2}) = \sum_{j=1}^{n}(\pi(p_{_{j+1}}^{2}) - \pi(p_{_{j}}^{2})) + \pi(p_{_{1}}^{2})$

$\pi_{_{H}}(p_{_{n+1}}^{2}) = p_{_{n+1}}^{2}.\prod_{i = 1}^{\pi(\sqrt{p_{_{n+1}}^{2}})}(1 - \frac{1}{p_{_{i}}})$

$= (\sum_{j=1}^{n}(p_{_{j+1}}^{2} - p_{_{j}}^{2}) + p_{_{1}}^{2}).\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}})$

$= \sum_{j=1}^{n}(p_{_{j+1}}^{2}.\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}}) - p_{_{j}}^{2}.\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}})) + p_{_{1}}^{2}.\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}})$

Since $\prod_{i = 1}^{n}(1 - \frac{1}{p_{_{i}}}) \rightarrow 0$ as $n \rightarrow \infty$ , we can, for any given $k$ , define $n_{_{k}} > k$ such that:

$\pi_{_{H}}(p_{_{n_{_{k}}+1}}^{2}) = \sum_{j=1}^{k}(p_{_{j+1}}^{2}.\prod_{i = 1}^{n_{_{k}}}(1 - \frac{1}{p_{_{i}}}) - p_{_{j}}^{2}.\prod_{i = 1}^{n_{_{k}}}(1 - \frac{1}{p_{_{i}}}))\ +$

$\sum_{j=k+1}^{n_{_{k}}}(p_{_{j+1}}^{2}.\prod_{i = 1}^{n_{_{k}}}(1 - \frac{1}{p_{_{i}}}) - p_{_{j}}^{2}.\prod_{i = 1}^{n_{_{k}}}(1 - \frac{1}{p_{_{i}}})) + p_{_{1}}^{2}.\prod_{i = 1}^{n_{_{k}}}(1 - \frac{1}{p_{_{i}}})$

$< \sum_{j=1}^{k}(\pi(p_{_{j+1}}^{2}) - \pi(p_{_{j}}^{2}))\ +$

We conclude that:

Theorem For any given $k$ , we can find $n_{_{k}} > k$ such that the estimated number $\pi_{_{H}}(p_{_{n_{_{k}}+1}}^{2})$ of primes $\leq p_{_{n_{_{k}}+1}}^{2}$ is always less than the actual number of primes less than $p_{_{k+1}}^{2}$ plus the number of primes between $p_{_{k+1}}^{2}$ and $p_{_{n_{_{k}}+1}}^{2}$ as estimated by $\pi_{_{H}}(p_{_{n_{_{k}}+1}}^{2})$ .

Since $\pi(n) \sim \frac{n}{log_{e}(n)}$ (by the Prime Number Theorem), whilst $\pi_{_{H}}(n) \sim 2e^{-\gamma}\frac{n}{log_{_{e}}n}$ (where $2.e^{-\gamma} \approx 1.12292 \ldots$ ), and $\pi_{_{L}}(n) > \pi_{_{H}}(n)$ for all $n \geq 9$ (see Figs.3 and 4), we note the apparent paradox:

Corollary The Prime Number Theorem implies that:

$\lim_{n \rightarrow \infty} \frac{\pi_{_{H}}(p_{_{n+1}}^{2})}{\pi(p_{_{n+1}}^{2})} = 2.e^{^{-\gamma}} > 1.$

3 Conventional estimates of $\pi(x)$ for finite $x > 2$ are heuristic

We note that Guy Robin (Robin, G. (1983). “Sur l’ordre maximum de la fonction somme des diviseurs”. Séminaire Delange-Pisot-Poitou, Théorie des nombres (1981-1982). Progress in Mathematics. 38: 233-244.) proved (implicit assumptions?) that the following changes sign infinitely often:

$(log_{e}\ n).\prod_{p \leq n}(1 - \frac{1}{p}) - e^{^{-\gamma}}$

Robin’s result is analogous to Littlewood’s curious theorem (implicit assumptions?) that the difference $\pi(x) - Li(x)$ changes sign infinitely often. No analogue of the Skewes number (an upper bound on the first natural number $x$ for which $\pi(x) > Li(x)$ ) is, however, known for Robin’s result.

Littlewood’s theorem is `curious’ since:

(a) There is no explicitly defined arithmetical formula that, for any $x > 2$ , will yield $\pi(x)$ . Hence, Littlewood’s proof deduces the behaviour of $\pi(x) - Li(x)$ for finite values of $x > 2$ by implicitly appealing to the relation of $\pi(x)$ to $\zeta(s)$ , defined as $\sum\frac{1}{n^{s}}$ over all integers $n \geq 1$ , through the identity of the infinite summation with the Euler product $\prod(1 - \frac{1}{p^{s}})^{^{-1}}$ over all primes, which is valid only for Re $(s) > 1$ ; as is its consequence (which involves the re-arrangement of an infinite summation that, too, is valid only for Re $(s) > 1$ ):

$log_{_{e}}\ \zeta(s) = s.\int_{_{2}}^{^{\infty}} \frac{\pi (x)}{x(x^{s}-1)}dx = s.\int_{_{2}}^{^{\infty}} \frac{\pi (x)/(1 - \frac{1}{x^{s}})}{x^{s+1}}dx$

(b) Littlewood’s proof deduces the behaviour of $\pi(x) - Li(x)$ for finite values of $x > 0$ by (uncritically, as I argue here?) appealing to the analytically continued behaviour of $\zeta(s)$ in areas where $\pi(x)$ is not defined!

Moreover, we note that—unlike $\pi_{_{H}}(n)$ and $\pi_{_{L}}(n)$ —conventional estimates of $\pi(x)$ for finite values of $x > 0$ can be treated as heuristic, since they appeal only to the limiting behaviour (Theorem 420, p.345, Hardy and Wright, Introduction to the Theory of Numbers, 4th ed, 1960, Oxford University Press) of a formally (i.e., explicitly) undefined arithmetical function, $\pi(n)$ , to the limiting behaviours of formally defined arithmetical functions $\phi(n)$ and $\psi(n)$ :

$\pi(x) \sim \frac{\phi(x)}{log_{_{e}}\ x} \sim \frac{\psi(x)}{log_{_{e}}\ x}$

where:

$\phi(x) = \sum_{_{p \leq x}}log_{_{e}}\ p = log_{_{e}} \prod_{_{p \leq x}}p$

$\psi(x) = \sum_{_{p^{m} \leq x}}log_{_{e}}\ p$

and, as detailed here, the latter is curiously stipulated as valid only for $x > 1$ , but definable in terms of a summation over the zeros of the zeta function in the critical strip $0 < R(\rho) < 1$ :

“ $\psi(x)$ is given by the so-called explicit formula

$\psi(x) = x - \sum_{_{\rho}} \frac{x^{^{\rho}}}{\rho} - log_{_{e}}\ (2.\pi) - \frac{1}{2}log_{_{e}}\ (1 - x^{^{2}})$

for $x > 1$ and $x$ not a prime or prime power, and the sum is over all nontrivial zeros $\rho$ of the Riemann zeta function $\zeta(s)$ , i.e., those in the critical strip so $0 < R(\rho) < 1$ , and interprets as

$lim_{_{t \rightarrow \infty}} \sum_{_{|I(\rho)| < t}} \frac{x^{^{\rho}}}{\rho}$ .”

Generating primes sequentially

May 15, 2016 in Foundations of mathematics, Foundations of mathematics, logic and computation, Philosophy, Theory of Numbers | Tags: algorithm, complete system of residues, computing, computational complexity, integer factorising, incongruent residues, mutually independent divisors, logic, modular arithmetic, natural number, number | Leave a comment

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

$\S 1$ Are there still unsolved problems about the numbers $1, 2, 3, 4, \ldots ?$

In a 2005 Clay Math Institute invited large lecture to a popular audience at MIT ‘Are there still unsolved problems about the numbers $1, 2, 3, 4, \ldots ?$ ’, co-author with William Stein of Prime Numbers and the Riemann Hypothesis, and Gerhard Gade Harvard University Professor, Barry Mazur remarked that (p.6):

“If I give you a number $N$ , say $N$ = one million, and ask you for the first number after $N$ that is prime, is there a method that answers that question without, in some form or other, running through each of the successive numbers after $N$ rejecting the nonprimes until the first prime is encountered? Answer: unknown.”

Although this may represent conventional wisdom, it is not, however, strictly true!

Reason: The following 1964 Theorem yields two algorithms (Trim/Compact), each of which affirmatively answers the questions:

(i) Do we necessarily discover the primes in a Platonic domain of the natural numbers, as is suggested by the sieve of Eratosthenes, or can we also generate them sequentially in a finitarily definable domain that builds into them the property of primality?

(ii) In other words, given the first $k$ primes, can we generate the prime $p(k+1)$ algorithmically, without testing any number larger than $p(k)$ for primality?

I: A PRIME NUMBER GENERATING THEOREM

Theorem: For all $i < k$ , let $p(i)$ denote the $i$ 'th prime, and define $a(i)$ such that:

$a(i) < p(i)$ ,

and:

$p(k) + a(i) \equiv 0\ (mod\ p(i))$ .

Let $d(k)$ be such that, for all $d < d(k)$ , there is some $i$ such that:

$d \equiv a(i)\ (mod\ p(i))$ .

Then:

$p(k+1) = p(k) + d(k)$ .

Proof: For all $d < d(k)$ , there is some $i$ such that:

$p(k) + d \equiv 0\ (mod\ p(i))$ .

Since $p(k+1) < 2p(k)$ :

$d(k) < p(k)$ .

Hence:

$p(k) + d(k) < p(k)^{2}$ ,

and so it is the prime $p(k+1)$ .

II: TRIM NUMBERS

The significance of the Prime Number Generating Theorem is seen in the following algorithm.

We define Trim numbers recursively by $t(1) = 2$ , and $t(n+1) = t(n) + d(n)$ , where $p(i)$ is the $i$ ‘th prime and:

(1) $d(1) = 1$ , and $a(2, 1) = 1$ is the only element in the $2$ nd array;

(2) $d(n)$ is the smallest even integer that does not occur in the $n$ ‘th array $\{a(n, 1), \ldots, a(n, n-1)\}$ ;

(3) $j$ is selected so that:

$0 \leq a(n+1, i) = (a(n, i) - d(n) + j*p(i) < p(i)$ for all $0 < i \leq (n-1)$ .

It follows that the Trim number $t(n+1)$ is, thus, a prime unless all its prime divisors are less than $d(n)$ .

The Trim Number Algorithm

$\line(1,0){285}$

n $t(n)$

1 2 2 3 5 7 11 13 17 19 23 27 29 31 37

$\line(1,0){285}$

2 3 1 $\textit{2}$ 5

3 5 1 1 $\textit{2}$ 7

4 7 1 2 3 $\textit{4}$ 11

5 11 1 1 4 3 $\textit{2}$ 13

6 13 1 2 2 1 9 $\textit{4}$ 17

7 17 1 1 3 4 5 9 $\textit{2}$ 19

8 19 1 2 1 2 3 7 15 $\textit{4}$ 23

9 23 1 1 2 5 10 3 11 15 $\textit{4}$ 27

10 27 1 0 3 1 6 12 7 11 19 $\textit{2}$ 29

11 29 1 1 1 6 4 10 5 9 17 $\textit{2}$ 31

$\ldots$

n $t(n)$ $r_{_{1}}$ $r_{_{2}}$ $r_{_{3}}$ $r_{_{4}}$ $r_{_{5}}$ $r_{_{6}}$ $r_{_{7}}$ $r_{_{8}}$ $r_{_{9}}$ $r_{_{10}}$ $r_{_{11}}$ … $\textit{\ldots}$

$\line(1,0){285}$

NOTE: The first $50$ Trim Numbers upto $t(50) = 199$ consist of the first $46$ primes and the $4$ composites:

(i) Trim composite $t(10)$ : $27 = 3.3.3$

(ii) Trim composite $t(32)$ : $125 = 5.5.5$

(iii) Trim composite $t(37)$ : $147 = 3.7.7$

(iv) Trim composite $t(46)$ : $189 = 3.3.3.7$

Theorem: For all $n > 1, t(n) < n^{^{2}}$

II A: $k$ -TRIM NUMBERS

For any given natural number $k>2$ , we define $k$ -Trim numbers recursively by $t_k(1) = 2$ , and $t_k(n+1) = t_k(n) + d(n)$ , where $p(i)$ is the $i$ ‘th prime and:

(1) $d(1) = 1$ , and $a(2, 1) = 1$ is the only element in the $2$ nd array;

(2) $d(n)$ is the smallest even integer that does not occur in the $n$ ‘th array $\{a(n, 1), \ldots, a(n, k-1)\}$ ;

(3) $j$ is selected so that:

$0 \leq a(n+1, i) = (a(n, i) - d(n) + j*p(i) < p(i)$ for all $0 < i \leq (k-1)$ .

It follows that the $k$ -Trim number $t_k(n+1)$ is, thus, not divisible by any prime $\leq p(k)$ unless the prime is smaller than $d(n)$ .

III: COMPACT NUMBERS

Compact numbers are defined recursively by $c(1) = 2$ , and $c(n+1) = c(n) + d(n)$ , where $p(i)$ is the $i$ ‘th prime and:

(1) $d(1) = 1$ , and $a(2, 1) = 1$ is the only element in the $2$ nd array;

(2) $d(n)$ is the smallest even integer that does not occur in the nth array $\{a(n, 1), \ldots, a(n, k)\}$ ;

(3) $j$ is selected so that:

$0 \leq a(n+1, i) = (a(n, i) - d(n) + j*p(i) < p(i)$ for all $0 < i \leq k$ ;

(4) $k$ is selected so that:

$p(k)*p(k) < c(n) \leq p(k+1)*p(k+1)$ ;

(5) $a(n, k+1) = 0$ if $c(n) = p(k+1)*p(k+1)$ .

It follows that the compact number $c(n+1)$ is either a prime, or a prime square, unless all, except a maximum of $1$ , prime divisors of the number are less than $d(n)$ .

The Compact Number Algorithm

$\line(1,0){285}$

n $c(n)$

1 2 2 3 5 7 11 13 17 19 23 29 31 37 41

$\line(1,0){285}$

2 3 1 $\textit{2}$ 5

3 5 1 $\textit{2}$ 7

4 7 1 $\textit{2}$ 9

5 9 1 0 $\textit{2}$ 11

6 11 1 1 $\textit{2}$ 13

7 13 1 2 $\textit{4}$ 17

8 17 1 1 $\textit{2}$ 19

9 19 1 2 $\textit{4}$ 23

10 23 1 1 $\textit{2}$ 25

11 25 1 2 0 $\textit{4}$ 29

12 29 1 1 1 $\textit{2}$ 31

13 31 1 2 4 $\textit{6}$ 37

14 37 1 2 3 $\textit{4}$ 41

15 41 1 1 4 $\textit{2}$ 43

16 43 1 2 2 $\textit{4}$ 47

17 47 1 1 3 $\textit{2}$ 49

18 49 1 2 1 0 $\textit{4}$ 53

19 53 1 1 2 3 $\textit{4}$ 57

20 57 1 0 3 6 $\textit{2}$ 59

21 59 1 1 1 4 $\textit{2}$ 61

22 61 1 2 4 2 $\textit{6}$ 67

23 67 1 2 3 3 $\textit{4}$ 71

24 71 1 1 4 6 $\textit{2}$ 73

25 73 1 2 2 4 $\textit{6}$ 79

26 79 1 2 1 5 $\textit{4}$ 83

27 83 1 1 2 1 $\textit{4}$ 87

28 87 1 0 3 4 $\textit{2}$ 89

29 89 1 1 1 2 $\textit{4}$ 93

30 93 1 0 2 5 $\textit{4}$ 97

31 97 1 2 3 1 $\textit{4}$ 101

32 101 1 1 4 4 $\textit{2}$ 103

33 103 1 2 2 2 $\textit{4}$ 107

34 107 1 1 3 5 $\textit{2}$ 109

35 109 1 2 1 3 $\textit{4}$ 113

36 113 1 1 2 6 $\textit{4}$ 117

37 117 1 0 3 2 $\textit{4}$ 121

38 121 1 2 4 5 0 $\textit{6}$ 127

39 127 1 2 3 6 5 $\textit{4}$ 131

40 131 1 1 4 2 1 $\textit{6}$ 137

41 137 1 1 3 3 6 $\textit{2}$ 139

42 139 1 2 1 1 4 $\textit{6}$ 145

43 145 1 2 0 2 9 $\textit{4}$ 149

44 149 1 1 1 5 5 $\textit{2}$ 151

45 151 1 2 4 5 0 $\textit{6}$ 157

46 157 1 2 3 4 8 $\textit{6}$ 163

47 163 1 2 2 5 2 $\textit{4}$ 167

48 167 1 1 3 1 9 $\textit{2}$ 169

49 169 1 2 1 6 7 0 $\textit{4}$ 173

50 173 1 1 2 2 3 9 $\textit{4}$ 177

51 177 1 0 3 5 10 5 $\textit{2}$ 179

52 179 1 1 1 3 8 3 $\textit{2}$ 181

53 181 1 2 4 1 6 1 $\textit{8}$ 189

54 189 1 0 1 0 9 6 $\textit{2}$ 191

55 191 1 1 4 5 7 4 $\textit{2}$ 193

56 193 1 2 2 3 5 2 $\textit{4}$ 197

57 197 1 1 3 6 1 11 $\textit{2}$ 199

58 199 1 2 1 4 10 9 $\textit{6}$ 205

59 205 1 2 0 5 4 3 $\textit{6}$ 211

60 211 1 2 4 6 9 10 $\textit{8}$ 219

61 219 1 0 1 5 1 2 $\textit{4}$ 223

62 223 1 2 2 1 8 11 $\textit{4}$ 227

63 227 1 1 3 4 4 7 $\textit{2}$ 229

64 229 1 2 1 2 2 5 $\textit{4}$ 233

65 233 1 1 2 5 9 14 $\textit{4}$ 237

66 237 1 0 3 1 5 10 $\textit{2}$ 239

67 239 1 1 1 6 3 8 $\textit{2}$ 241

68 241 1 2 4 4 1 6 $\textit{8}$ 249

69 249 1 0 1 3 4 11 $\textit{2}$ 251

70 251 1 1 4 1 2 9 $\textit{6}$ 257

71 257 1 1 3 2 7 3 $\textit{4}$ 261

72 261 1 0 4 5 3 12 $\textit{2}$ 263

73 263 1 1 2 3 1 10 $\textit{4}$ 267

74 267 1 0 3 6 8 6 $\textit{2}$ 269

75 269 1 1 1 4 6 4 $\textit{2}$ 271

76 271 1 2 4 2 4 2 $\textit{6}$ 277

77 277 1 2 3 3 9 9 $\textit{4}$ 281

78 281 1 1 4 6 5 5 $\textit{2}$ 283

79 283 1 2 2 4 3 3 $\textit{6}$ 289

$\ldots$

n $c(n)$ $r_{_{1}}$ $r_{_{2}}$ $r_{_{3}}$ $r_{_{4}}$ $r_{_{5}}$ $r_{_{6}}$ $r_{_{7}}$ $r_{_{8}}$ $r_{_{9}}$ $r_{_{10}}$ $r_{_{11}}$ …

$\line(1,0){285}$

NOTE: The first $79$ Compact Numbers upto $c(79) = 283$ consist of the first $61$ primes, $5$ prime squares, and $13$ composites.

Theorem 1: There is always a Compact Number $c(m)$ such that $n^{^{2}} < c(m) \leq (n+1)^{^{2}}$ .

Theorem 2: For sufficiently large $n,\ d(n) < constant.\frac{\sqrt{c(n)}}{log_{_{e}}c(n)}$ .

$\S 2$ A 2-dimensional Eratosthenes sieve

A later investigation (see also this post) shows why the usual, linearly displayed, Eratosthenes sieve argument reveals the structure of divisibility (and, ipso facto, of primality) more transparently when displayed as the 1964, $2$ -dimensional matrix, representation of the residues $r_{i}(n)$ , defined for all $n \geq 2$ and all $i \geq 2$ by:

$n + r_{i}(n) \equiv 0\ (mod\ i)$ , where $i > r_{i}(n) \geq 0$ .

‘Density‘: For instance, the residues $r_{_{i}}(n)$ can be defined for all $n \geq 1$ as the values of the non-terminating sequences $Ri (n) = \{i-1, i-2, \ldots, 0, i-1, i-2, \ldots, 0, \ldots\}$ , defined for all $i \geq 1$ (as illustrated below in Fig.1).

Fig.1

$\line(1,0){285}$

Sequence $R_{_{1}}$ $R_{_{2}}$ $R_{_{3}}$ $R_{_{4}}$ $R_{_{5}}$ $R_{_{6}}$ $R_{_{7}}$ $R_{_{8}}$ $R_{_{9}}$ $R_{_{10}}$ $R_{_{11}}$ … $R_{_{n}}$

$\line(1,0){285}$

n=1 $\textbf{0}$ 1 2 3 4 5 6 7 8 9 10 … n-1

n=2 0 $\textbf{0}$ 1 2 3 4 5 6 7 8 9 … n-2

n=3 0 1 $\textbf{0}$ 1 2 3 4 5 6 7 8 … n-3

n=4 0 0 2 $\textbf{0}$ 1 2 3 4 5 6 7 … n-4

n=5 0 1 1 3 $\textbf{0}$ 1 2 3 4 5 6 … n-5

n=6 0 0 0 2 4 $\textbf{0}$ 1 2 3 4 5 … n-6

n=7 0 1 2 1 3 5 $\textbf{0}$ 1 2 3 4 … n-7

n=8 0 0 1 0 2 4 6 $\textbf{0}$ 1 2 3 … n-8

n=9 0 1 0 3 1 3 5 7 $\textbf{0}$ 1 2 … n-9

n=10 0 0 2 2 0 2 4 6 8 $\textbf{0}$ 1 … n-10

n=11 0 1 1 1 4 1 3 5 7 9 $\textbf{0}$ … n-11

$\ldots$

n $r_{_{1}}$ $r_{_{2}}$ $r_{_{3}}$ $r_{_{4}}$ $r_{_{5}}$ $r_{_{6}}$ $r_{_{7}}$ $r_{_{8}}$ $r_{_{9}}$ $r_{_{10}}$ $r_{_{11}}$ … $\textbf{0}$

$\line(1,0){285}$

We note that:

$\bullet$ For any $i \geq 2$ , the non-terminating sequence $R_{_{i}}(n)$ cycles through the values $(i-1, i-2, \ldots 0)$ with period $i$ ;

$\bullet$ For any $i \geq 2$ the ‘density’—over the set of natural numbers—of the set $\{n\}$ of integers that are divisible by $i$ is $\frac{1}{i}$ ; and the ‘density’ of integers that are not divisible by $i$ is $\frac{i-1}{i}$ .

Primality: The residues $r_{_{i}}(n)$ can be alternatively defined for all $i \geq 1$ as values of the non-terminating sequences, $E(n) = \{r_{_{i}}(n) : i \geq 1\}$ , defined for all $n \geq 1$ (as illustrated below in Fig.2).

Fig.2

$\line(1,0){285}$

Sequence $R_{_{1}}$ $R_{_{2}}$ $R_{_{3}}$ $R_{_{4}}$ $R_{_{5}}$ $R_{_{6}}$ $R_{_{7}}$ $R_{_{8}}$ $R_{_{9}}$ $R_{_{10}}$ $R_{_{11}}$ … $R_{_{n}}$

$\line(1,0){285}$

$E(1)$ $\textbf{0}$ 1 2 3 4 5 6 7 8 9 10 … n-1

$\textbf{E(2)}$ 0 $\textbf{0}$ 1 2 3 4 5 6 7 8 9 … n-2

$\textbf{E(3)}$ 0 1 $\textbf{0}$ 1 2 3 4 5 6 7 8 … n-3

$\textit{E(4)}$ 0 0 2 $\textbf{0}$ 1 2 3 4 5 6 7 … n-4

$\textbf{E(5)}$ 0 1 1 3 $\textbf{0}$ 1 2 3 4 5 6 … n-5

$\textit{E(6)}$ 0 0 0 2 4 $\textbf{0}$ 1 2 3 4 5 … n-6

$\textbf{E(7)}$ 0 1 2 1 3 5 $\textbf{0}$ 1 2 3 4 … n-7

$\textit{E(8)}$ 0 0 1 0 2 4 6 $\textbf{0}$ 1 2 3 … n-8

$\textit{E(9)}$ 0 1 0 3 1 3 5 7 $\textbf{0}$ 1 2 … n-9

$\textit{E(10)}$ 0 0 2 2 0 2 4 6 8 $\textbf{0}$ 1 … n-10

$\textbf{E(11)}$ 0 1 1 1 4 1 3 5 7 9 $\textbf{0}$ … n-11

$\ldots$

$E(n)$ $r_{_{1}}$ $r_{_{2}}$ $r_{_{3}}$ $r_{_{4}}$ $r_{_{5}}$ $r_{_{6}}$ $r_{_{7}}$ $r_{_{8}}$ $r_{_{9}}$ $r_{_{10}}$ $r_{_{11}}$ … $\textbf{0}$

$\line(1,0){285}$

We note that:

$\bullet$ The non-terminating sequences $\textbf{E(n)}$ highlighted in bold correspond to a prime $p$ (since $r_{_{i}}(p) \neq 0$ for any $1 < i < p$ ) in the usual, linearly displayed, Eratosthenes sieve:

$E(1), \textbf{E(2)}, \textbf{E(3)}, \textit{E(4)}, \textbf{E(5)}, \textit{E(6)}, \textbf{E(7)}, \textit{E(8)}, \textit{E(9)}, \textit{E(10)}, \textbf{E(11)}, \ldots$

$\bullet$ The non-terminating sequences $\textit{E(n)}$ highlighted in italics identify a crossed out composite $n$ (since $r_{_{i}}(n) = 0$ for some $1 < i < n$ ) in the usual, linearly displayed, Eratosthenes sieve.

The significance of expressing Eratosthenes sieve as a $2$ -dimensional matrix

Fig.1 illustrates that although the probability $P(a)$ of selecting a number that has the property of being prime from a given set $S$ of numbers is definable if the precise proportion of primes to non-primes in $S$ is definable, if $S$ is the set $N$ of all integers, and we cannot define a precise ratio of primes to composites in $N$ , but only an order of magnitude such as $O(\frac{1}{log_{_{e}}n})$ , then equally obviously $P(a) = P(n\ is\ a\ prime)$ cannot be defined in $N$ (see Chapter 2, p.9, Theorem 2.1, here).

The probability $P(b)$ of determining a proper factor of a given number $n$

Fig.2 illustrates, however, that the probability $P(b)$ of determining a proper factor of a given number $n$ is $\frac{1}{\pi(\sqrt{n})}$ , since this paper shows that whether or not a prime $p$ divides a given integer $n$ is independent of whether or not a prime $q \neq p$ divides $n$ .

We thus have that $\pi(n) \approx n.\prod_{_{i = 1}}^{^{\pi(\sqrt{n})}}(1-\frac{1}{p_{_{i}}})$ .

The putative non-heuristic probability that a given $n$ is a prime

$\S 3$ “What sort of Hypothesis is the Riemann Hypothesis?”

The significance of the above perspective is that (see this investigation) it admits non-heuristic approximations of prime counting functions (see Fig.15 of the investigation) where:

“It has long been known that that for any real number $X$ the number of prime numbers less than $X$ (denoted $\pi(X))$ is approximately $X/ log X$ in the sense that the ratio $\frac{\pi(X)}{X/ log X}$ tends to $1$ as $X$ goes to infinity. The Riemann Hypothesis would give us a much more accurate “count” for $\pi(X)$ in that it will offer a specific smooth function $R(X)$ (hardly any more difficult to describe than $X/ log X$ ) and then conjecture that $R(X)$ is an essentially square root accurate approximation to $\pi(X)$ ; i.e., for any given exponent greater than $1/2$ (you choose it: $0.501,\ 0.5001,\ 0.50001$ , for example) and for large enough $X$ where the phrase “large enough” depends on your choice of exponent the error term i.e., the difference between $R(X)$ and the number of primes less than $X$ in absolute value is less than $X$ raised to that exponent (e.g. $< X^{0.501}, < X^{0.5001}$ , etc.)"

… Barry Mazur and William Stein, ‘What is Riemann’s Hypothesis‘

The Prime Number Theorem

July 7, 2014 in Foundations of mathematics, logic and computation, Theory of Numbers | Tags: algorithm, complete system of residues, incongruent residues, integer factorising, logic, modular arithmetic, mutually independent divisors, natural number, number theory, pi, prime divisor, Prime Number Theorem, prime number theorem PNT, probability of n being a prime | Leave a comment

This argument laid the foundation for this investigation. See also this arXiv preprint, and this broader update.

Abstract We define the residues $r_{i}(n)$ for all $n \geq 2$ and all $i \geq 2$ such that $r_{i}(n) = 0$ if, and only if, $i$ is a divisor of $n$ . We then show that the joint probability $\mathbb{P}(p_{i} | n\ \cap\ p_{j} | n)$ of two unequal primes $p_{i},\ p_{j}$ dividing any integer $n$ is the product $\mathbb{P}(p_{i} | n).\mathbb{P}(p_{j} | n)$ . We conclude that the prime divisors of any integer $n$ are independent; and that the probability $\mathbb{P}(n \in \{p\})$ of $n$ being a prime $p$ is $\prod_{i = 1}^{\sqrt{n}}(1 - 1/p_{i}) \sim 2e^{-\gamma}/log_{e}\ n$ . The number of primes less than or equal to $n$ is thus given by $\pi(n) \approx \sum_{j = 1}^{n}\prod_{i = 1}^{\pi(\sqrt{j})}(1 - 1/p_{i})$ . We further show that $((\pi(x).log_{e}\ x)/x)' = o(1/x)$ , and conclude that $(\pi(x).log_{e}\ x)/x$ does not oscillate.

$\S 1$ The residues $r_{i}(n)$

We begin by defining the residues $r_{i}(n)$ for all $n \geq 2$ and all $i \geq 2$ as below:

Definition 1: $n + r_{i}(n) \equiv 0\ (mod\ i)$ where $i > r_{i}(n) \geq 0$ .

Since each residue $r_{i}(n)$ cycles over the $i$ values $(i-1, i-2, \ldots, 0)$ , these values are all incongruent and form a complete system of residues ^[1] $mod\ i$ .

It immediately follows that:

Lemma 1: $r_{i}(n) = 0$ if, and only if, $i$ is a divisor of $n$ .

$\S 2$ The probability $\mathbb{P}(e)$

By the standard definition of the probability $\mathbb{P}(e)$ of an event $e$ , we conclude that:

Lemma 2: For any $n \geq 2,\ i \geq 2$ and any given integer $i > u \geq 0$ , the probability $\mathbb{P}(r_{i}(n) = u)$ that $r_{i}(n) = u$ is $1/i$ , and the probability $\mathbb{P}(r_{i}(n) \neq u)$ that $r_{i}(n) \neq u$ is $1 - 1/i$ .

We note the standard definition:

Definition 2: Two events $e_{i}$ and $e_{j}$ are mutually independent for $i \neq j$ if, and only if, $\mathbb{P}(e_{i}\ \cap\ e_{j}) = \mathbb{P}(e_{i}).\mathbb{P}(e_{j})$ .

$\S 3$ The prime divisors of any integer $n$ are mutually independent

We then have that:

Lemma 3: If $p_{i}$ and $p_{j}$ are two primes where $i \neq j$ then, for any $n \geq 2$ , we have:

$\mathbb{P}((r_{p_{_{i}}}(n) = u) \cap (r_{p_{_{j}}}(n) = v)) = \mathbb{P}(r_{p_{_{i}}}(n) = u).\mathbb{P}(r_{p_{_{j}}}(n) = v)$

where $p_{i} > u \geq 0$ and $p_{j} > v \geq 0$ .

Proof: The $p_{i}.p_{j}$ numbers $v.p_{i} + u.p_{j}$ , where $p_{i} > u \geq 0$ and $p_{j} > v \geq 0$ , are all incongruent and form a complete system of residues ^[2] $mod\ (p_{i}.p_{j})$ . Hence:

$\mathbb{P}((r_{p_{_{i}}}(n) = u) \cap (r_{p_{_{j}}}(n) = v)) = 1/p_{i}.p_{j}$ .

By Lemma 2:

$\mathbb{P}(r_{p_{_{i}}}(n) = u).\mathbb{P}(r_{p_{_{j}}}(n) = v) = (1/p_{i})(1/p_{j})$ .

The lemma follows. $\Box$

If $u = 0$ and $v = 0$ in Lemma 3, so that both $p_{i}$ and $p_{j}$ are prime divisors of $n$ , we conclude by Definition 2 that:

Corollary 1: $\mathbb{P}((r_{p_{_{i}}}(n) = 0) \cap (r_{p_{_{j}}}(n) = 0)) = \mathbb{P}(r_{p_{_{i}}}(n) = 0).\mathbb{P}(r_{p_{_{j}}}(n) = 0)$ .

Corollary 2: $\mathbb{P}(p_{i} | n\ \cap\ p_{j} | n) = \mathbb{P}(p_{i} | n).\mathbb{P}(p_{j} | n)$ .

Theorem 1: The prime divisors of any integer $n$ are mutually independent. ^[3]

$\S 4$ The probability that $n$ is a prime

Since $n$ is a prime if, and only if, it is not divisible by any prime $p \leq \sqrt{n}$ , it follows immediately from Lemma 2 and Lemma 3 that:

Lemma 4: For any $n \geq 2$ , the probability $\mathbb{P}(n \in \{p\})$ of an integer $n$ being a prime $p$ is the probability that $r_{p_{_{i}}}(n) \neq 0$ for any $1 \leq i \leq k$ if $p_{k}^{2} \leq n < p_{k+1}^{2}$ . $\Box$

Lemma 5: $\mathbb{P}(n \in \{p\}) = \prod_{i = 1}^{\pi(\sqrt{n})}(1 - 1/p_{i}) \sim 2e^{-\gamma}/log_{e}\ n$ ^[4]. $\Box$

$\S 5$ The Prime Number Theorem

The number of primes less than or equal to $n$ is thus given by:

Lemma 6: $\pi(n) \approx \sum_{j = 1}^{n}\prod_{i = 1}^{\pi(\sqrt{j})}(1 - 1/p_{i})$ . $\Box$

This now yields the Prime Number Theorem:

Theorem 2: $\pi(x) \sim x/log_{e}\ x$ .

Proof: From Lemma 6 and Mertens’ Theorem that
^[5]:

$\prod_{p \leq x}(1 - 1/p_{i}) = e^{o(1)}.e^{-\gamma}/log_{e}\ x$

it follows that:

$(\pi(n).log_{e}\ n)/n \approx (log_{e}\ n/n)\sum_{j = 1}^{n}\prod_{i = 1}^{\pi(\sqrt{j})}(1 - 1/p_{i})$

$(\pi(n).log_{e}\ n)/n \approx (log_{e}\ n/n)\sum_{j = 1}^{n}(2.e^{o(1)}.e^{-\gamma})/log_{e}\ n$

$(\pi(x).log_{e}\ x)/x \sim c.(log_{e}\ x/x)\int_{2}^{x}(1/log_{e}\ t).dt$

$(\pi(x).log_{e}\ x)/x \sim c.(log_{e}\ x/x)[log_{e}.log_{e}\ t + log_{e}\ t + \sum_{2}^{\infty}(log_{e}\ t)^{k}/(k. k!)]_{2}^{^{x}}$

$(\pi(x).log_{e}\ x)/x \sim c.(log_{e}\ x/x)[log_{e}.log_{e}\ x + log_{e}\ x + \sum_{2}^{\infty}(log_{e}\ x)^{k}/(k. k!)]$

$(\pi(x).log_{e}\ x)/x \sim c.(log_{e}\ x/x).f(log_{e}\ x)$

The behaviour of $(\pi(x).log_{e}\ x)/x$ as $x \rightarrow \infty$ is then seen by differentiating the right hand side, where we note that $f(log_{e}\ x)' = 1/log_{e}\ x$ :

$(c.(log_{e}\ x/x).f(log_{e}\ x))' = c/x + c.f(log_{e}\ x).(1/x^{2} - log_{e}\ x/x^{2})$

$(c.(log_{e}\ x/x).f(log_{e}\ x))' = c/x + (c.f(log_{e}\ x).(1 - log_{e}\ x))/x^{2}$

$(c.(log_{e}\ x/x).f(log_{e}\ x))' = o(1/x)$

Hence $(\pi(x).log_{e}\ x)/x$ does not oscillate as $x \rightarrow \infty$ . $\Box$

Acknowledgements

I am indebted to my erstwhile classmate, Professor Chetan Mehta, for his unqualified encouragement and support for my scholarly pursuits over the past fifty years; most pertinently for his patiently critical insight into the required rigour without which the argument of this 1964 investigation would have remained in the informal universe of seemingly self-evident truths.

References

HW60 G. H. Hardy and E. M. Wright. 1960. An Introduction to the Theory of Numbers 4th edition. Clarendon Press, Oxford.

Ti51 E. C. Titchmarsh. 1951. The Theory of the Riemann Zeta-Function. Clarendon Press, Oxford.

Notes

Return to 1: HW60, p.49.

Return to 2: HW60, p.52, Theorem 59.

Return to 3: In the previous post we have shown how it immediately follows from Theorem 1 that integer factorising is necessarily of order $O(n/log_{e}\ n)$ ; from which we conclude that integer factorising cannot be in the class $P$ of polynomial-time algorithms.

Return to 4: By HW60, p.351, Theorem 429, Mertens’ Theorem.

Return to 5: By the argument in Ti51, p.59, eqn.(3.15.2).

Return to 6: HW60, p.9, Theorem 7.

Author’s working archives & abstracts of investigations

Follow me on Academia.edu

Integer Factorising is not in P

July 2, 2014 in Foundations of mathematics, logic and computation, Theory of Numbers | Tags: algorithm, complete system of residues, computational complexity, computing, incongruent residues, integer factorising, logic, modular arithmetic, mutually independent divisors, natural number, number theory, polynomial-time, prime divisor, prime generating algorithms, probability of n being a prime, PvNP | Leave a comment

This argument laid the foundation for this later post and this investigation.

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

Abstract: We show the joint probability $\mathbb{P}(p_{i} | n\ \cap\ p_{j} | n)$ that two unequal primes $p_{i},\ p_{j}$ divide any integer $n$ is the product $\mathbb{P}(p_{i} | n).\mathbb{P}(p_{j} | n)$ . We conclude that the prime divisors of any integer $n$ are independent; and that Integer Factorising is necessarily of the order $O(n/log_{e}\ n)$ .

$\S 1$ The residues $r_{i}(n)$

We define the residues $r_{i}(n)$ for all $n \geq 2$ and all $i \geq 2$ as below:

Definition 1: $n + r_{i}(n) \equiv 0\ (mod\ i)$ where $i > r_{i}(n) \geq 0$ .

Since each residue $r_{i}(n)$ cycles over the $i$ values $(i-1, i-2, \ldots, 0)$ , these values are all incongruent and form a complete system of residues ^[1] $mod\ i$ .

We note that:

Lemma 1: $r_{i}(n) = 0$ if, and only if, $i$ is a divisor of $n$ .

$\S 2$ The probability $\mathbb{P}(e)$

By the standard definition of the probability ^[2] $\mathbb{P}(e)$ of an event $e$ , we then have that:

We note the standard definition ^[3]:

Definition 2: Two events $e_{i}$ and $e_{j}$ are mutually independent for $i \neq j$ if, and only if, $\mathbb{P}(e_{i}\ \cap\ e_{j}) = \mathbb{P}(e_{i}).\mathbb{P}(e_{j})$ .

$\S 3$ The prime divisors of any integer $n$ are mutually independent

We then have that:

Lemma 3: If $p_{i}$ and $p_{j}$ are two primes where $i \neq j$ then, for any $n \geq 2$ , we have:

$\mathbb{P}((r_{p_{_{i}}}(n) = u) \cap (r_{p_{_{j}}}(n) = v)) = \mathbb{P}(r_{p_{_{i}}}(n) = u).\mathbb{P}(r_{p_{_{j}}}(n) = v)$

where $p_{i} > u \geq 0$ and $p_{j} > v \geq 0$ .

Proof: The $p_{i}.p_{j}$ numbers $v.p_{i} + u.p_{j}$ , where $p_{i} > u \geq 0$ and $p_{j} > v \geq 0$ , are all incongruent and form a complete system of residues ^[4] $mod\ (p_{i}.p_{j})$ . Hence:

$\mathbb{P}((r_{p_{_{i}}}(n) = u) \cap (r_{p_{_{j}}}(n) = v)) = 1/p_{i}.p_{j}$ .

By Lemma 2:

$\mathbb{P}(r_{p_{_{i}}}(n) = u).\mathbb{P}(r_{p_{_{j}}}(n) = v) = (1/p_{i})(1/p_{j})$ .

The lemma follows. $\Box$

If $u = 0$ and $v = 0$ in Lemma 3, so that both $p_{i}$ and $p_{j}$ are prime divisors of $n$ , we conclude by Definition 2 that:

Corollary 1: $\mathbb{P}((r_{p_{_{i}}}(n) = 0) \cap (r_{p_{_{j}}}(n) = 0)) = \mathbb{P}(r_{p_{_{i}}}(n) = 0).\mathbb{P}(r_{p_{_{j}}}(n) = 0)$ .

Corollary 2: $\mathbb{P}(p_{i} | n\ \cap\ p_{j} | n) = \mathbb{P}(p_{i} | n).\mathbb{P}(p_{j} | n)$ .

Theorem 1: The prime divisors of any integer $n$ are mutually independent.

Since $n$ is a prime if, and only if, it is not divisible by any prime $p \leq \sqrt{n}$ we may, without any loss of generality, take integer factorising to mean determining at least one prime factor $p \leq \sqrt{n}$ of any given $n \geq 2$ .

$\S 4$ Integer Factorising is not in $P$

It then immediately follows from Theorem 1 that:

Corollary 3: Integer Factorising is not in $P$ .

Proof: We note that any computational process to identify a prime divisor of $n \geq 2$ must necessarily appeal to a logical operation for identifying such a factor.

Since $n$ may be the square of a prime, it follows from Theorem 1 that we necessarily require at least one logical operation for each prime $p \leq \sqrt{n}$ in order to logically identify a prime divisor of $n$ .

Moreover, since the number of such primes is of the order $O(n/log_{e}\ n)$ , any deterministic algorithm that always computes a prime factor of $n$ cannot be polynomial-time—i.e. of order $O((log_{e}\ n)^{c})$ for any $c$ —in the length of the input $n$ .

The corollary follows if $P$ is the set of such polynomial-time algorithms. $\Box$

Acknowledgements

References

GS97 Charles M. Grinstead and J. Laurie Snell. 1997. Introduction to Probability. Second Revised Edition, 1997, American Mathematical Society, Rhode Island, USA.

HW60 G. H. Hardy and E. M. Wright. 1960. An Introduction to the Theory of Numbers 4th edition. Clarendon Press, Oxford.

Ko56 A. N. Kolmogorov. 1933. Foundations of the Theory of Probability. Second English Edition. Translation edited by Nathan Morrison. 1956. Chelsea Publishing Company, New Yourk.

An05 Bhupinder Singh Anand. 2005. Three Theorems on Modular Sieves that suggest the Prime Difference is $O(\pi(p(n)^{1/2}))$ . Private investigation.

Notes

Return to 1: HW60, p.49.

Return to 2: Ko56, Chapter I, Section 1, Axiom III, p.2; see also GS97, Chapter 1, Section 1.2, Definition 1.2, p.19.

Return to 3: Ko56, Chapter VI, Section 1, Definition 1, pg.57 and Section 2, pg.58; see also GS97, Chapter 4, Section 4.1, Theorem 4.1, pg.140.

Return to 4: HW60, p.52, Theorem 59.

Author’s working archives & abstracts of investigations

A Highly Speculative Post About Speculation: Defining Market Equilibrium in a Simplified Stock Exchange

November 29, 2013 in Economic Theory, Foundations of mathematics, logic and computation, Philosophy, Theory of Numbers | Tags: algorithmically computable, algorithmically verifiable, cabal, computational complexity, economic theory, equilibrium distribution, feasible, inflationary, John F. Muth, Lyapunov function, maintenance charge, market equilibrium, PvNP, Robert Axtell, scrip, Social Welfare Function, socio-proctologist, speculation, speculator, stock market, transaction cost, transaction fee, transaction tax, Travelling Salesman Problem, valuation, Walrasian equilibrium | 1 comment

In this post we shall beg indulgence for wilfully ignoring Wittgenstein’s dictum: “Whereof one cannot speak, thereof one must be silent.”

(Notations, non-standard concepts, and definitions used commonly in these investigations are detailed in this post.)

$\S 1$ The Background

In his comments on this earlier post (on the need for a better consensus on the definition of `effective computability‘) socio-proctologist Vivek Iyer—who apparently prefers to be known here only through this blogpage, and whose sustained interest has almost compelled a more responsible response in the form of this blogpage—raised an interesting query (albeit obliquely) on whether commonly accepted Social Welfare Functions—such as those based on Muth rationality—could possibly be algorithmically verifiable, but not algorithmically computable:

“We know the mathematical properties of market solutions but assume we can know the Social Welfare Function which brought it about. We have the instantiation and know it is computable but we don’t know the underlying function.”

He later situated the query against the perspective of:

“… the work of Robert Axtell http://scholar.google.com/citations?user=K822uYQAAAAJ&hl=en- who has derived results for the computational complexity class of market (Walrasian) eqbm. This is deterministically computable as a solution for fixed points in exponential time, though easily or instantaneously verifiable (we just check that the market clears by seeing if there is anyone who still wants to sell or buy at the given price). Axtell shows that bilateral trades are complexity class P and this is true of the Subjective probabilities.”

Now, the key para of Robert Axtell’s paper seemed to be:

“The second welfare theorem states that any Pareto optimal allocation is a Walrasian equilibrium from some endowments, and is usually taken to mean that a social planner/society can select the allocation it wishes to achieve and then use tax and related regulatory policy to alter endowments such that subsequent market processes achieve the allocation in question. We have demonstrated above that the job of such a social planner would be very hard indeed, and here we ask whether there might exist a computationally more credible version of the second welfare theorem”…Axtell p.9

Axtell’s aim here seemed to be to maximise in polynomial time the Lyapunov function $V(x(t))$ (given on Axtell p.7; which is a well-defined number-theoretic formula over the real numbers) to within a specific range of its limiting value over a given set of possible endowment allocations.

Distribution of Resources

Prima facie Axtell’s problem seemed to lie within a general class of problems concerning the distribution of finite resources amongst a finite population.

For instance, the total number of ways, say $P(n, k)$ in which any budgeted measure of $n$ discrete endowments can be allocated over $k$ agents is given by the partition function $P(n, k)$ (which I wrongly commented upon as being the factorisation function $F(n, k)$ generated by $\eta_{k}(s)$ ):

$\prod_{i=1}^{\infty}\frac{1}{(1-ax^{i})} = \sum_{n=1}^{\infty}\sum_{k=1}^{\infty}P(n, k)a^{k}x^{n}$

We noted that if we take one of the allocations $E$ as the equilibrium (ideal/desired destination) distribution, then a general problem of arriving at an ideal Distribution of Resources from a given starting distribution could ask whether there is always a path that is polynomial in $P(n, k)$ and such that, starting from any arbitrary distribution, there is a minimum cost for passing (in the worst case) through all the possible distributions irreversibly (where we assume that it is not feasible under any series of individual rational exchanges for a particular resource distribution over the population to repeat itself with time).

We assumed there that, for any given set of distributions $S_{i}=\{A_{1},\ A_{2},\ \ldots,\ A_{i}\}$ and any $A_{j}$ , there is a minimum measure $m_{S_{i}S_{j}}$ which determines the cost of progressing from the set of distributions $A_{i}=\{A_{1},\ A_{2},\ \ldots,\ A_{i}\}$ to the set of distributions $S_{j}=\{A_{1},\ A_{2},\ \ldots,\ A_{j}\}$ , where $A_{j}$ is not in $S_{i}=\{A_{1},\ A_{2},\ \ldots,\ A_{i}\}$ .

We noted that mathematically the above can be viewed as a variation of the Travelling Salesman problem where the goal is to minimise the total cost of progressing from a starting distribution $A_{1}$ to the ideal distribution $E$ , under the influence of free market forces based on individual rational exchanges that are only regulated to ensure—through appropriate taxation and/or other economic tools—that the cost of repeating a distribution is not feasible.

We further noted that, since the Travelling Salesman Problem is in the complexity class $NP$ , it would be interesting to identify where exactly Axtell’s problem reduces to the computability complexity class $P$ (and where we ignore, for the moment, the $PvNP$ separation problem raised in this earlier post).

$\S 2$ Defining Market Equilibrium in a Simplified Stock Exchange

In order to get a better perspective on the issue of an equilibrium, we shall now speculate on whether we can reasonably define a market equilibrium in a simplified terminating market situation (i.e., a situation which always ends when there is no possible further profitable activity for any participant), where our definition of an equilibrium is any terminal state of minimum total cost and maximum total gain.

For instance, we could treat the population in question as a simplified on-line Stock Exchange with $k$ speculators $B_{1},\ B_{2},\ \ldots, B_{k}$ and $n$ scrips, where both $k$ and $n$ are fixed.

Now we can represent a distribution $A_{(t)}$ at time $t$ by one of the ways, say $P(n,\ k)$ , in which $n$ can be partitioned into $k$ parts as $n = a_{i} + a_{2} + \ldots + a_{k}$ , where $a_{i}$ is the number of scrips (mandatorily $\geq 1$ ) held by speculator $B{i}$ at time $t$ (which can fluctuate freely based on market forces of supply and demand).

We note that the generating function for $P(n,\ k)$ is given by the partition function:

$\prod_{i=1}^{\infty}\frac{1}{(1-ax^{i})} = \sum_{n=1}^{\infty}\sum_{k=1}^{\infty}P(n, k)a^{k}x^{n}$

One could then conceive of a Transaction Corpus Tax ( $TCT$ ) as a cess on each transaction levied by the Regulator (such as India’s SEBI) on the Exchange:

$\bullet$ Where $TCT$ is directly recovered by the Exchange from individual speculators along with an appropriate Transaction Processing Fee ( $TPF$ ) and a periodic Exchange Maintenance Cost ( $EMC$ ); and

$\bullet$ Where, unless the market is in a terminating situation, the maintenance charge $EMC$ is uniformly leviable periodically, even if no transaction has taken place, to ensure that trading activity never halts voluntarily.

Now, given an initial distribution, say $A_{0}$ , of the scrips amongst the population $k$ , we can assume that any transaction by say speculator $B_{i}$ at time $t_{j}$ would incur a $TCT$ cost $f_{t_{j}}(A_{j},\ A_{j+1})$ , plus a $TPF$ and a (possibly discounted) $EMC$ .

Obviously the gain to $B_{i}$ must exceed $TCT+TPF+EMC$ for the trade to be a rational one.

However, what is important to note here (which obviously need not apply in dissimilar cases such as Axtell’s) is that apparently none of the following factors:

(a) the price of the scrip being traded at any transaction;

(b) the quantum of the gain (which need not even be quantifiable in any particular transaction);

seem to play any role in reaching the Equilibrium Distribution $E_{(n,\ k)}$ for the particular set of $k$ speculators $\{B_{1},\ B_{2},\ \ldots,\ B_{k}\}$ and $n$ scrips.

Moreover, the only restriction is on $TCT$ , to the effect that:

$f_{t_{i}}(A_{i},\ A_{j}) = \infty$ for any $i$ if $j < i$

In other words, no transaction can take place that requires a distribution to be repeated.

One way of justifying such a Regulatory restriction would be that if a distribution were allowed to repeat itself, a cabal could prevent market equilibrium by artificially fuelling speculation aimed at merely inflating the valuations of the $n$ scrips over a selected distribution.

By definition, starting with any distribution $A_{0}$ , it would seem that the above activity must come to a mandatory halt after having passed necessarily through all the possible $P(k,\ n)$ distributions.

If so, this would reduce the above to a Travelling Salesman Problem TSP if we define the Equilibrium Distribution $E_{(n,\ k)}$ as the (not necessarily unique) distribution which minimises the Total Transaction Corpus Tax to speculators in reaching the Equilibrium through all possible distributions.

In other words, the Equilibrium Distribution is—by definition—the one for which $\sum_{i=0}^{P(n,\ k)} f_{t_{i}}(A_{i},\ A_{i+1})$ is a minimum; and is one that can be shown to always exist.

$\S 3$ What do you think (an afterthought)?

Assuming all the speculators $B_{1},\ B_{2},\ \ldots, B_{k}$ agree that their individual profitability can only be assured over a terminating distribution cycle if, and only if, the Total Transaction Corpus Tax $\sum_{i=0}^{P(n,\ k)} f_{t_{i}}(A_{i},\ A_{i+1})$ is minimised (not an unreasonable agreement to seek in a country like India that once had punitive 98% rates of Income Tax), can $E_{(n,\ k)}$ be interpreted as a Nash equilibrium?

In other words, in the worst case where the quantum of Transaction Corpus Tax can be arbitrarily revised and levied with retrospective effect at any transaction, is there a Nash strategy that can guide the set $B_{1},\ B_{2},\ \ldots, B_{k}$ of speculators into ensuring that they eventually arrive at an Equilibrium Distribution $E_{(n,\ k)}$ ?

References

Ax03 Robert Axtell. 2003. The Complexity of Exchange. In Econometrica, Vol. 29, No. 3 (July 1961).

Mu61 John F. Muth. 1961. Rational Expectations and the Theory of Price Movements. In Econometrica, Vol. 29, No. 3 (July 1961).

	Abel Peralta on Can Gödel be held guilty of im…
	Bhupinder Singh Anan… on Can Gödel be held guilty of im…
	Abel Peralta on Can Gödel be held guilty of im…
	Bhupinder Singh Anan… on Why Gödel’s Theorem…
	Abel Peralta on Why Gödel’s Theorem…

Category Archive

The significance of evidence-based reasoning for Computational Complexity

Why the prime divisors of an integer are mutually independent

Why there are infinitely many twin primes

Can Primes yield a heuristic model of quantum behaviour?

The PvNP problem: Why we need to review current approaches towards determining the computational complexity of Integer Factorising

Three intriguing non-heuristic prime counting function queries

Generating primes sequentially

The Prime Number Theorem

Integer Factorising is not in P

Readability

Start here

Follow Blog via Email

Search

Recent posts

Blogs I Follow

Recent comments